Teorema lui De Moivre – Laplace - De Moivre–Laplace theorem

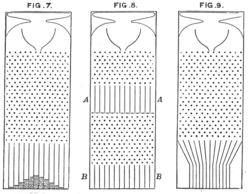
Într-un sistem ale cărui coșuri sunt umplute în funcție de distribuția binomială (cum ar fi " mașina de fasole " a lui Galton , prezentată aici), a fost dat un număr suficient de încercări (aici rândurile de știfturi, fiecare dintre ele determină căderea unei "fasole" căzută spre stânga sau dreapta), o formă care reprezintă distribuția probabilității de k succese în n studii (vezi partea de jos a Fig. 7) se potrivește aproximativ cu distribuția Gaussiană cu media np și varianța np (1− p ), presupunând că studiile sunt independente și succesele apar cu probabilitate p .

Luați în considerare aruncarea unui set de n monede de un număr foarte mare de ori și numărarea numărului de „capete” care rezultă de fiecare dată. Numărul posibil de capete pe fiecare aruncare, k , rulează de la 0 la n de -a lungul axei orizontale, în timp ce axa verticală reprezintă frecvența relativă de apariție a rezultatelor k capete. Înălțimea fiecărui punct este astfel probabilitatea de a observa k capete atunci când aruncați n monede (o distribuție binomială bazată pe n încercări). Conform teoremei de Moivre – Laplace, pe măsură ce n crește, forma distribuției discrete converge către curba gaussiană continuă a distribuției normale .

În teoria probabilității , teorema de Moivre – Laplace , care este un caz special al teoremei limitei centrale , afirmă că distribuția normală poate fi utilizată ca o aproximare la distribuția binomială în anumite condiții. În special, teorema arată că funcția de masă a probabilității numărului aleatoriu de „succese” observate într-o serie de studii Bernoulli independente , fiecare având probabilitate de succes (o distribuție binomială cu studii), converge la funcția densității probabilității normalului distribuție cu deviație medie și standard , pe măsură ce crește, presupunând că nu este sau . ${\ displaystyle n}$ ${\ displaystyle p}$${\ displaystyle n}$${\ displaystyle np}$${\ textstyle {\ sqrt {np (1-p)}}}$${\ displaystyle n}$${\ displaystyle p}$${\ displaystyle 0}$${\ displaystyle 1}$

Teorema a apărut în cea de-a doua ediție a Doctrinei șanselor de Abraham de Moivre , publicată în 1738. Deși de Moivre nu a folosit termenul „încercări Bernoulli”, el a scris despre distribuția probabilității numărului de ori în care apare „capetele” atunci când o monedă este aruncată de 3600 de ori.

Aceasta este o derivare a funcției Gaussiene utilizate în distribuția normală.

Teorema

Pe măsură ce n crește, pentru k în vecinătatea lui np putem aproxima

${\ displaystyle {n \ choose k} \, p ^ {k} q ^ {nk} \ simeq {\ frac {1} {\ sqrt {2 \ pi npq}}} \, e ^ {- {\ frac { (k-np) ^ {2}} {2npq}}}, \ qquad p + q = 1, \ p, q> 0}$

în sensul că raportul dintre partea stângă și partea dreaptă converge la 1 ca n → ∞.

Dovadă

Teorema poate fi enunțată mai riguros după cum urmează :, cu o variabilă aleatorie distribuită binomial, se apropie de normalul standard ca , raportul dintre masa probabilității și densitatea normală limitativă fiind 1. Acest lucru poate fi arătat pentru un arbitrar diferit de zero și finit punct . Pe curba nescalată pentru , acesta ar fi un punct dat de ${\ displaystyle \ left (X \! \, - \! \, np \ right) \! / \! {\ sqrt {npq}}}$${\ displaystyle \ textstyle X}$${\ displaystyle n \! \ to \! \ infty}$${\ displaystyle X}$${\ displaystyle c}$${\ displaystyle X}$${\ displaystyle k}$

${\ displaystyle k = np + c {\ sqrt {npq}}}$

De exemplu, cu la 3, rămâne 3 abateri standard de la medie în curba nescalată. ${\ displaystyle c}$${\ displaystyle k}$

Distribuția normală cu deviația medie și standard este definită de ecuația diferențială (DE) ${\ displaystyle \ mu}$${\ displaystyle \ sigma}$

${\ displaystyle f '\! (x) \! = \! - \! \, {\ frac {x- \ mu} {\ sigma ^ {2}}} f (x)}$cu condiția inițială stabilită de axioma probabilității .${\ displaystyle \ int _ {- \ infty} ^ {\ infty} \! f (x) \, dx \! = \! 1}$

Limita de distribuție binomială se apropie de normal dacă binomul satisface acest DE. Deoarece binomul este discret, ecuația începe ca o ecuație de diferență a cărei limită se transformă în DE. Ecuațiile de diferență utilizează derivata discretă ,, schimbarea pentru mărimea pasului 1. Deoarece , derivata discretă devine derivată continuă . Prin urmare, necesitatea dovezilor arată doar că, pentru distribuția binomială nescalată, ${\ displaystyle \ textstyle p (k \! + \! 1) \! - \! p (k)}$${\ displaystyle \ textstyle n \! \ to \! \ infty}$

${\ displaystyle {\ frac {f '\! (x)} {f \! (x)}} \! \ cdot \! \ left (- {\ frac {\ sigma ^ {2}} {x- \ mu }} \ right) \! \ to \! 1}$ca .${\ displaystyle n \! \ to \! \ infty}$

Rezultatul necesar poate fi afișat direct:

${\ displaystyle {\ begin {align} {\ frac {f '\! (x)} {f \! (x)}} {\ frac {npq} {np \! \, - \! \, k}} \! & = {\ frac {p \ left (n, k + 1 \ right) -p \ left (n, k \ right)} {p \ left (n, k \ right)}} {\ frac {\ sqrt {npq}} {- c}} \\ & = {\ frac {np-kq} {kq + q}} {\ frac {\ sqrt {npq}} {- c}} \\ & = {\ frac {-c {\ sqrt {npq}} - q} {npq + cq {\ sqrt {npq}} + q}} {\ frac {\ sqrt {npq}} {- c}} \\ & \ to 1 \ sfârșit {aliniat}}}$

Ultima deține , deoarece termenul domină atât numitorul și numărătorul . ${\ displaystyle -cnpq}$${\ displaystyle n \! \ to \! \ infty}$

Deoarece ia doar valori integrale, constanta este supusă unei erori de rotunjire. Cu toate acestea, maximul acestei erori ,, este o valoare de dispariție. ${\ displaystyle \ textstyle k}$${\ displaystyle \ textstyle c}$${\ displaystyle \ textstyle {0.5} / \! {\ sqrt {npq}}}$

Dovezi alternative

Dovada constă în transformarea laturii stângi (în enunțul teoremei) în partea dreaptă prin trei aproximări.

În primul rând, conform formulei lui Stirling , factorialul unui număr mare n poate fi înlocuit cu aproximarea

${\ displaystyle n! \ simeq n ^ {n} e ^ {- n} {\ sqrt {2 \ pi n}} \ qquad {\ text {as}} n \ to \ infty.}$

Prin urmare

${\ displaystyle {\ begin {align} {n \ choose k} p ^ {k} q ^ {nk} & = {\ frac {n!} {k! (nk)!}} p ^ {k} q ^ {nk} \\ & \ simeq {\ frac {n ^ {n} e ^ {- n} {\ sqrt {2 \ pi n}}} {k ^ {k} e ^ {- k} {\ sqrt { 2 \ pi k}} (nk) ^ {nk} e ^ {- (nk)} {\ sqrt {2 \ pi (nk)}}}} p ^ {k} q ^ {nk} \\ & = { \ sqrt {\ frac {n} {2 \ pi k \ left (nk \ right)}} {\ frac {n ^ {n}} {k ^ {k} \ left (nk \ right) ^ {nk} }} p ^ {k} q ^ {nk} \\ & = {\ sqrt {\ frac {n} {2 \ pi k \ left (nk \ right)}}} \ left ({\ frac {np} { k}} \ right) ^ {k} \ left ({\ frac {nq} {nk}} \ right) ^ {nk} \ end {align}}}$

Apoi, aproximarea este utilizată pentru a potrivi rădăcina de mai sus cu rădăcina dorită din partea dreaptă. ${\ displaystyle {\ tfrac {k} {n}} \ to p}$

${\ displaystyle {\ begin {align} {n \ choose k} p ^ {k} q ^ {nk} & \ simeq {\ sqrt {\ frac {1} {2 \ pi n {\ frac {k} {n }} \ left (1 - {\ frac {k} {n}} \ right)}}} \ left ({\ frac {np} {k}} \ right) ^ {k} \ left ({\ frac { nq} {nk}} \ right) ^ {nk} \\ & \ simeq {\ frac {1} {\ sqrt {2 \ pi npq}}} \ left ({\ frac {np} {k}} \ right ) ^ {k} \ left ({\ frac {nq} {nk}} \ right) ^ {nk} \ qquad p + q = 1 \\\ end {align}}}$

În cele din urmă, expresia este rescrisă ca exponențială și se utilizează aproximarea seriei Taylor pentru ln (1 + x):

${\ displaystyle \ ln \ left (1 + x \ right) \ simeq x - {\ frac {x ^ {2}} {2}} + {\ frac {x ^ {3}} {3}} - \ cdots }$

Atunci

${\ displaystyle {\ begin {align} {n \ choose k} p ^ {k} q ^ {nk} & \ simeq {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {\ ln \ left (\ left ({\ frac {np} {k}} \ right) ^ {k} \ right) + \ ln \ left (\ left ({\ frac {nq} {nk}} \ right ) ^ {nk} \ right) \ right \} \\ & = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {- k \ ln \ left ({\ frac { k} {np}} \ right) + (kn) \ ln \ left ({\ frac {nk} {nq}} \ right) \ right \} \\ & = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {- k \ ln \ left ({\ frac {np + x {\ sqrt {npq}}} {np}} \ right) + (kn) \ ln \ left ( {\ frac {n-np-x {\ sqrt {npq}}} {nq}} \ right) \ right \} \\ & = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {- k \ ln \ left ({1 + x {\ sqrt {\ frac {q} {np}}}} \ right) + (kn) \ ln \ left ({1-x {\ sqrt {\ frac {p} {nq}}} \ right) \ right \} \ qquad p + q = 1 \\ & = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {- k \ left ({x {\ sqrt {\ frac {q} {np}}}} - {\ frac {x ^ {2} q} {2np}} + \ cdots \ right) + (kn ) \ left ({- x {\ sqrt {\ frac {p} {nq}}} - {\ frac {x ^ {2} p} {2nq}}} - \ cdots \ right) \ right \} \\ & = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {\ left (-np-x {\ sqrt {npq}} \ right) \ left ({x {\ sqrt {\ frac {q} {np}}}} - {\ frac {x ^ {2} q} {2np}} + \ cdots \ righ t) + \ left (np + x {\ sqrt {npq}} - n \ right) \ left (-x {\ sqrt {\ frac {p} {nq}}} - {\ frac {x ^ {2} p} {2nq}} - \ cdots \ right) \ right \} \\ & = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {\ left (-np-x {\ sqrt {npq}} \ right) \ left (x {\ sqrt {\ frac {q} {np}}} - {\ frac {x ^ {2} q} {2np}} + \ cdots \ right) - \ left (nq-x {\ sqrt {npq}} \ right) \ left (-x {\ sqrt {\ frac {p} {nq}}} - {\ frac {x ^ {2} p} {2nq }} - \ cdots \ right) \ right \} \\ & = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {\ left (-x {\ sqrt {npq} } + {\ frac {1} {2}} x ^ {2} qx ^ {2} q + \ cdots \ right) + \ left (x {\ sqrt {npq}} + {\ frac {1} {2} } x ^ {2} px ^ {2} p- \ cdots \ right) \ right \} \\ & = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {- {\ frac {1} {2}} x ^ {2} q - {\ frac {1} {2}} x ^ {2} p- \ cdots \ right \} \\ & = {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {- {\ frac {1} {2}} x ^ {2} (p + q) - \ cdots \ right \} \\ & \ simeq {\ frac {1} {\ sqrt {2 \ pi npq}}} \ exp \ left \ {- {\ frac {1} {2}} x ^ {2} \ right \} \\ & = {\ frac {1} {\ sqrt {2 \ pi npq}}} e ^ {\ frac {- (k-np) ^ {2}} {2npq}} \\\ end {align}}}$

Fiecare „ ” din argumentul de mai sus este o afirmație conform căreia două mărimi sunt echivalente asimptotic pe măsură ce n crește, în același sens ca în enunțul original al teoremei - adică, raportul fiecărei perechi de mărimi se apropie de 1 ca n → ∞. ${\ displaystyle \ simeq}$

Trivia

• Zidul este un exemplu de emisiune de jocuri de televiziunecare folosește teorema De Moivre – Laplace.

Vezi si

• Distribuția Poisson este o aproximare alternativă a distribuției binomiale pentru valori mari de n .

Note