Funcții eliptice Jacobi - Jacobi elliptic functions

În matematică , funcțiile eliptice Jacobi sunt un set de funcții eliptice de bază și funcții theta auxiliare , care sunt de importanță istorică. Ele se găsesc în descrierea mișcării unui pendul (vezi și pendul (matematică) ), precum și în proiectarea filtrelor eliptice electronice . În timp ce funcțiile trigonometrice sunt definite cu referire la un cerc, funcțiile eliptice Jacobi sunt o generalizare care se referă la alte secțiuni conice , în special elipsa. Relația cu funcțiile trigonometrice este conținută în notație, de exemplu, prin notația potrivită${\ displaystyle \ operatorname {sn}}$pentru . Funcțiile eliptice Jacobi sunt utilizate mai des în problemele practice decât funcțiile eliptice Weierstrass, deoarece nu necesită noțiuni de analiză complexă pentru a fi definite și / sau înțelese. Au fost introduse de Carl Gustav Jakob Jacobi  ( 1829 ). ${\ displaystyle \ sin}$

Prezentare generală

Dreptunghiul fundamental în planul complex al ${\ displaystyle u}$

Există douăsprezece Jacobi funcții eliptic notate cu , în cazul în care și sunt oricare dintre litere , , și . (Funcțiile formei sunt setate în mod trivial la unitate pentru completitudinea noțională.) Este argumentul și este parametrul, ambele putând fi complexe. ${\ displaystyle \ operatorname {pq} (u, m)}$${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$${\ displaystyle \ mathrm {c}}$${\ displaystyle \ mathrm {s}}$${\ displaystyle \ mathrm {n}}$${\ displaystyle \ mathrm {d}}$${\ displaystyle \ operatorname {pp} (u, m)}$${\ displaystyle u}$${\ displaystyle m}$

În planul complex al argumentului , cele douăsprezece funcții formează o rețea repetată de poli simpli și zerouri . În funcție de funcția, un paralelogram repetitivă, sau celula unitate, va avea laturile de o lungime sau pe axa reală, și sau pe axa imaginară, în cazul în care și sunt cunoscute ca perioadele trimestru cu fiind integrala eliptică de primul tip. Natura celulei unitare poate fi determinată prin inspectarea „dreptunghiului auxiliar” (în general un paralelogram), care este un dreptunghi format de origine la un colț și ca colț opus diagonal. Ca și în diagrama, cele patru colțuri ale dreptunghiului auxiliare sunt numite , , , și , mergând în sens antiorar de origine. Funcția va avea un zero la colț și un stâlp la colț. Cele douăsprezece funcții corespund celor douăsprezece moduri de aranjare a acestor poli și zerouri în colțurile dreptunghiului. ${\ displaystyle u}$${\ displaystyle 2K}$${\ displaystyle 4K}$${\ displaystyle 2K '}$${\ displaystyle 4K '}$${\ displaystyle K = K (m)}$${\ displaystyle K '= K (1-m)}$${\ displaystyle K (\ cdot)}$${\ displaystyle (0,0)}$${\ displaystyle (K, K ')}$${\ displaystyle \ mathrm {s}}$${\ displaystyle \ mathrm {c}}$${\ displaystyle \ mathrm {d}}$${\ displaystyle \ mathrm {n}}$${\ displaystyle \ operatorname {pq} (u, m)}$${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$

Când argumentul și parametrul sunt reale, cu , și va fi real și paralelogramului auxiliar va fi de fapt un dreptunghi, iar funcțiile eliptic Jacobi vor fi evaluate toate reale pe linia reală. ${\ displaystyle u}$${\ displaystyle m}$${\ displaystyle 0 <m <1}$${\ displaystyle K}$${\ displaystyle K '}$

Matematic, funcțiile eliptice iacobiene sunt funcții meromorfe dublu periodice pe planul complex . Deoarece sunt dublu periodice, ele factorează printr-un tor - efectiv, domeniul lor poate fi considerat un tor, la fel cum cosinusul și sinusul sunt definite efectiv pe un cerc. În loc să avem un singur cerc, acum avem produsul a două cercuri, unul real și celălalt imaginar. Planul complex poate fi înlocuit cu un tor complex . Circumferința primului cerc este și a doua , unde și sunt perioadele de sfert . Fiecare funcție are două zerouri și doi poli în poziții opuse pe tor. Printre punctele , , , există un zero și un pol. ${\ displaystyle 4K}$${\ displaystyle 4K '}$${\ displaystyle K}$${\ displaystyle K '}$${\ displaystyle 0}$${\ displaystyle K}$${\ displaystyle K + iK '}$${\ displaystyle iK '}$

Funcțiile eliptice iacobiene sunt apoi funcțiile meromorfe unice dublu periodice care îndeplinesc următoarele trei proprietăți:

• Există un zero simplu la colț și un stâlp simplu la colț  .${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$
• Pasul de la la este egal cu jumătate din perioada funcției ; adică funcția este periodică în direcție , perioada fiind de două ori distanța de la la . Funcția este, de asemenea, periodică în celelalte două direcții, cu o perioadă astfel încât distanța de la unul dintre celelalte colțuri să fie de un sfert de perioadă.${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$${\ displaystyle \ operatorname {pq} u}$${\ displaystyle \ operatorname {pq} u}$${\ displaystyle \ operatorname {pq}}$${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$${\ displaystyle \ operatorname {pq} u}$${\ displaystyle \ mathrm {p}}$
• Dacă funcția este extinsă în termeni de la unul dintre colțuri, termenul principal în expansiune are un coeficient de  . Cu alte cuvinte, termenul principal al extinderii de la colț este ; termenul principal al expansiunii la colț este , iar termenul principal al expansiunii la celelalte două colțuri este  .${\ displaystyle \ operatorname {pq} u}$${\ displaystyle u}$${\ displaystyle 1}$${\ displaystyle \ operatorname {pq} u}$${\ displaystyle \ mathrm {p}}$${\ displaystyle u}$${\ displaystyle \ mathrm {q}}$${\ displaystyle u ^ {- 1}}$${\ displaystyle 1}$

Funcția eliptică Jacobi ${\ displaystyle \ operatorname {sn}}$

Funcția eliptică Jacobi ${\ displaystyle \ operatorname {cn}}$

Funcția eliptică Jacobi ${\ displaystyle \ operatorname {dn}}$

Funcția eliptică Jacobi ${\ displaystyle \ operatorname {sc}}$

Diagramele a patru funcții eliptice Jacobi în planul complex al , ilustrând comportamentul lor dublu periodic. Imagini generate folosind o versiune a metodei de colorare a domeniului . Toate au valori ale parametrului egale cu .${\ displaystyle u}$${\ displaystyle k}$${\ displaystyle 0.8}$

Notaţie

Funcțiile eliptice pot fi date într-o varietate de notații, ceea ce poate face subiectul în mod inutil confuz. Funcțiile eliptice sunt funcții ale două variabile. Prima variabilă poate fi dată în termeni de amplitudine , sau mai frecvent, în termeni de mai jos. A doua variabilă ar putea fi dată în termeni de parametru , sau ca modul eliptic , unde , sau în termeni de unghi modular , unde . Complementele și sunt definite ca și . Acești patru termeni sunt folosiți mai jos fără comentarii pentru a simplifica diferite expresii. ${\ displaystyle \ varphi}$${\ displaystyle u}$ ${\ displaystyle m}$ ${\ displaystyle k}$${\ displaystyle k ^ {2} = m}$ ${\ displaystyle \ alpha}$${\ displaystyle m = \ sin ^ {2} \ alpha}$${\ displaystyle k}$${\ displaystyle m}$${\ displaystyle m '= 1-m}$${\ textstyle k '= {\ sqrt {m'}}}$

Cele douăsprezece Jacobi funcții eliptic sunt în general scrise ca în cazul în care și sunt oricare dintre litere , , , și . Funcțiile formei sunt setate în mod trivial la unitate pentru completitudinea noțională. Funcțiile „majore“ sunt , în general , considerată a fi , și din care toate celelalte funcții pot fi derivate și expresii sunt scrise adesea numai în ceea ce privește aceste trei funcții, cu toate acestea, diferite simetrii și generalizări sunt adesea exprimate mai convenabil folosind setul complet. (Această notație se datorează Gudermann și Glaisher și nu este notația originală a lui Jacobi.) ${\ displaystyle \ operatorname {pq} (u, m)}$${\ displaystyle \ mathrm {p}}$${\ displaystyle \ mathrm {q}}$${\ displaystyle \ mathrm {c}}$${\ displaystyle \ mathrm {s}}$${\ displaystyle \ mathrm {n}}$${\ displaystyle \ mathrm {d}}$${\ displaystyle \ operatorname {pp} (u, m)}$${\ displaystyle \ operatorname {cn} (u, m)}$${\ displaystyle \ operatorname {sn} (u, m)}$${\ displaystyle \ operatorname {dn} (u, m)}$

Parametrul

Funcțiile sunt relaționate în mod notational între ele prin regula multiplicării: (argumentele suprimate)

${\ displaystyle \ operatorname {pq} \ cdot \ operatorname {p'q '} = \ operatorname {pq'} \ cdot \ operatorname {p'q}}$

din care pot fi derivate alte relații frecvent utilizate:

${\ displaystyle {\ frac {\ operatorname {pr}} {\ operatorname {qr}}} = \ operatorname {pq}}$

${\ displaystyle \ operatorname {pr} \ cdot \ operatorname {rq} = \ operatorname {pq}}$

${\ displaystyle {\ frac {1} {\ operatorname {qp}}} = \ operatorname {pq}}$

Regula multiplicării urmează imediat din identificarea funcțiilor eliptice cu funcțiile theta Neville

${\ displaystyle \ operatorname {pq} (u, m) = {\ frac {\ theta _ {\ operatorname {p}} (u, m)} {\ theta _ {\ operatorname {q}} (u, m) }}}$

Definiție ca inversele integralelor eliptice

Model de amplitudine (măsurat de-a lungul axei verticale) în funcție de variabilele independente u și k

Definiția de mai sus, în ceea ce privește funcțiile meromorfe unice care îndeplinesc anumite proprietăți, este destul de abstractă. Există o definiție mai simplă, dar complet echivalentă, care dă funcțiilor eliptice ca inversuri ale integralei eliptice incomplete de primul fel. Lăsa

${\ displaystyle u = \ int _ {0} ^ {\ varphi} {\ frac {\ mathrm {d} \ theta} {\ sqrt {1-m \ sin ^ {2} \ theta}}} \ ,.}$

Apoi sinusul eliptic sn  u (latin: sinus amplitudinis ) este dat de

${\ displaystyle \ operatorname {sn} u = \ sin \ varphi \,}$

iar cosinusul eliptic cn  u (latin: cosinus amplitudinis ) este dat de

${\ displaystyle \ operatorname {cn} u = \ cos \ varphi}$

și amplitudinea delta dn  u (latină: delta amplitudinis )

${\ displaystyle \ operatorname {dn} u = {\ sqrt {1-m \ sin ^ {2} \ varphi}} \ ,.}$

Aici, unghiul se numește amplitudine . Ocazional, se numește amplitudinea delta . În cele de mai sus, valoarea este un parametru liber, de obicei considerat a fi real, și astfel funcțiile eliptice pot fi considerate ca fiind date de două variabile, amplitudinea și parametrul  . ${\ displaystyle \ varphi}$${\ displaystyle \ operatorname {dn} u = \ Delta (u)}$${\ displaystyle m}$${\ displaystyle 0 \ leq m \ leq 1}$${\ displaystyle \ varphi}$${\ displaystyle m}$

Restul de nouă funcții eliptice sunt ușor de construit din cele trei de mai sus și sunt prezentate într-o secțiune de mai jos.

Rețineți că atunci când , atunci u este egal cu perioada trimestrială . ${\ displaystyle \ varphi = \ pi / 2}$ ${\ displaystyle K}$

Definiție ca trigonometrie: elipsa Jacobi

Traseul elipsei Jacobi ( x ² + y ² / b ² = 1, b real) și cele douăsprezece funcții eliptice Jacobi pq (u, m) pentru valori particulare ale unghiului φ și parametrului b . Curba solidă este elipsa, cu m = 1-1 / b ² și u = F (φ, m) unde F (.,.) Este integrala eliptică de primul fel. Curba punctată este cercul unitar. Liniile tangente din cerc și elipsa la x = cd care traversează axa x la dc sunt prezentate în gri deschis.

${\ displaystyle \ cos \ varphi, \ sin \ varphi}$sunt definite pe cercul unitar, cu raza r  = 1 și lungimea arcului unghiular al cercului unitar măsurat din axa x pozitivă . În mod similar, funcțiile eliptice Jacobi sunt definite pe elipsa unității, cu a  = 1. Fie ${\ displaystyle \ varphi =}$

${\ displaystyle {\ begin {align} & x ^ {2} + {\ frac {y ^ {2}} {b ^ {2}}} = 1, \ quad b> 1, \\ & m = 1 - {\ frac {1} {b ^ {2}}}, \ quad 0 <m <1, \\ & x = r \ cos \ varphi, \ quad y = r \ sin \ varphi \ end {align}}}$

atunci:

${\ displaystyle r (\ varphi, m) = {\ frac {1} {\ sqrt {1-m \ sin ^ {2} \ varphi}}} \ ,.}$

Pentru fiecare unghi parametrul ${\ displaystyle \ varphi}$

${\ displaystyle u = u (\ varphi, m) = \ int _ {0} ^ {\ varphi} r (\ theta, m) \, d \ theta}$

este calculat. Pe cercul unității ( ), ar fi o lungime a arcului. Deși nu pare să poarte o interpretare geometrică directă în cazul eliptic, se dovedește a fi parametrul care intră în definiția funcțiilor eliptice. Într-adevăr, să fie un punct pe elipsă și să fie punctul în care cercul unității intersectează linia dintre și origine . Apoi relațiile familiare din cercul unității: ${\ displaystyle a = b = 1}$${\ displaystyle u}$${\ displaystyle u}$${\ displaystyle P = (x, y) = (r \ cos \ varphi, r \ sin \ varphi)}$${\ displaystyle P '= (x', y ') = (\ cos \ varphi, \ sin \ varphi)}$${\ displaystyle P}$${\ displaystyle O}$

${\ displaystyle x '= \ cos \ varphi, \ quad y' = \ sin \ varphi}$

citiți pentru elipsă:

${\ displaystyle x '= \ operatorname {cn} (u, m), \ quad y' = \ operatorname {sn} (u, m).}$

Deci, proiecțiile punctului de intersecție ale liniei cu cercul unitar pe x - și y- yax sunt pur și simplu și . Aceste proiecții pot fi interpretate ca „definiție ca trigonometrie”. În scurt: ${\ displaystyle P '}$${\ displaystyle OP}$${\ displaystyle \ operatorname {cn} (u, m)}$${\ displaystyle \ operatorname {sn} (u, m)}$

${\ displaystyle \ operatorname {cn} (u, m) = {\ frac {x} {r (\ varphi, m)}}, \ quad \ operatorname {sn} (u, m) = {\ frac {y} {r (\ varphi, m)}}, \ quad \ operatorname {dn} (u, m) = {\ frac {1} {r (\ varphi, m)}}.}$

Pentru și valoarea punctului cu și parametru obținem, după inserarea relației: ${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle P}$${\ displaystyle u}$${\ displaystyle m}$

${\ displaystyle r (\ varphi, m) = {\ frac {1} {\ operatorname {dn} (u, m)}}}$

în: că: ${\ displaystyle x = r (\ varphi, m) \ cos (\ varphi), y = r (\ varphi, m) \ sin (\ varphi)}$

${\ displaystyle x = {\ frac {\ operatorname {cn} (u, m)} {\ operatorname {dn} (u, m)}}, \ quad y = {\ frac {\ operatorname {sn} (u, m)} {\ operatorname {dn} (u, m)}}.}$

Ultimele relații pentru coordonatele x - și y ale punctelor de pe elipsa unității pot fi considerate ca generalizare a relațiilor pentru coordonatele punctelor de pe cercul unității. ${\ displaystyle x = \ cos \ varphi, y = \ sin \ varphi}$

Tabelul următor rezumă expresiile pentru toate funcțiile eliptice Jacobi pq (u, m) din variabilele ( x , y , r ) și ( φ , dn) cu${\ displaystyle r = {\ sqrt {x ^ {2} + y ^ {2}}}}$

Funcțiile eliptice Jacobi pq [u, m] ca funcții ale lui {x, y, r} și {φ, dn}

		q
		c	s	n	d
p
	c	1	${\ displaystyle x / y = \ cot (\ phi)}$	${\ displaystyle x / r = \ cos (\ phi)}$	${\ displaystyle x = \ cos (\ phi) / \ operatorname {dn}}$
	s	${\ displaystyle y / x = \ tan (\ phi)}$	1	${\ displaystyle y / r = \ sin (\ phi)}$	${\ displaystyle y = \ sin (\ phi) / \ operatorname {dn}}$
	n	${\ displaystyle r / x = \ sec (\ phi)}$	${\ displaystyle r / y = \ csc (\ phi)}$	1	${\ displaystyle r = 1 / \ operatorname {dn}}$
	d	${\ displaystyle 1 / x = \ operatorname {dn} \ sec (\ phi)}$	${\ displaystyle 1 / y = \ operatorname {dn} \ csc (\ phi)}$	${\ displaystyle 1 / r = \ operatorname {dn}}$	1

Definiție în termeni de funcții theta Jacobi

În mod echivalent, funcțiile eliptice ale lui Jacobi pot fi definite în funcție de funcțiile sale theta . Dacă prescurtăm ca și respectiv ca ( constantele theta ) atunci modulul eliptic k al funcției theta este . Dacă stabilim , avem ${\ displaystyle \ vartheta (0; \ tau)}$${\ displaystyle \ vartheta}$${\ displaystyle \ vartheta _ {01} (0; \ tau), \ vartheta _ {10} (0; \ tau), \ vartheta _ {11} (0; \ tau)}$${\ displaystyle \ vartheta _ {01}, \ vartheta _ {10}, \ vartheta _ {11}}$ ${\ displaystyle k = \ left ({\ vartheta _ {10} \ over \ vartheta} \ right) ^ {2}}$${\ displaystyle u = \ pi \ vartheta ^ {2} z}$

${\ displaystyle {\ begin {align} \ operatorname {sn} (u; k) & = - {\ vartheta \ vartheta _ {11} (z; \ tau) \ over \ vartheta _ {10} \ vartheta _ {01 } (z; \ tau)} \\ [7pt] \ operatorname {cn} (u; k) & = {\ vartheta _ {01} \ vartheta _ {10} (z; \ tau) \ over \ vartheta _ { 10} \ vartheta _ {01} (z; \ tau)} \\ [7pt] \ operatorname {dn} (u; k) & = {\ vartheta _ {01} \ vartheta (z; \ tau) \ over \ vartheta \ vartheta _ {01} (z; \ tau)} \ end {align}}}$

Deoarece funcțiile Jacobi sunt definite în termeni de modul eliptic , trebuie să inversăm acest lucru și să găsim în termeni de . Începem de la modulul complementar . În funcție de aceasta este ${\ displaystyle k (\ tau)}$${\ displaystyle \ tau}$${\ displaystyle k}$${\ displaystyle k '= {\ sqrt {1-k ^ {2}}}}$${\ displaystyle \ tau}$

${\ displaystyle k '(\ tau) = \ left ({\ vartheta _ {01} \ over \ vartheta} \ right) ^ {2}.}$

Să definim mai întâi

${\ displaystyle \ ell = {1 \ over 2} {1 - {\ sqrt {k '}} \ over 1 + {\ sqrt {k'}}} = {1 \ over 2} {\ vartheta - \ vartheta _ {01} \ over \ vartheta + \ vartheta _ {01}}.}$

Apoi definiți numele ca și extindeți-vă ca o serie de putere în nome , obținem ${\ displaystyle q = \ exp (\ pi i \ tau)}$${\ displaystyle \ ell}$${\ displaystyle q}$

${\ displaystyle \ ell = {q + q ^ {9} + q ^ {25} + \ cdots \ over 1 + 2q ^ {4} + 2q ^ {16} + \ cdots}.}$

Reversiunea seriei dă acum

${\ displaystyle q = \ ell +2 \ ell ^ {5} +15 \ ell ^ {9} +150 \ ell ^ {13} +1707 \ ell ^ {17} +20910 \ ell ^ {21} +268616 \ ell ^ {25} + \ cdots.}$

Deoarece putem reduce la cazul în care partea imaginară a este mai mare sau egală cu , putem presupune că valoarea absolută a este mai mică sau egală cu ; pentru valori atât de mici, seria de mai sus converge foarte rapid și ne permite cu ușurință să găsim valoarea potrivită pentru . ${\ displaystyle \ tau}$${\ displaystyle {\ sqrt {3}} / 2}$${\ displaystyle q}$${\ displaystyle \ exp (- \ pi {\ sqrt {3}} / 2) \ aproximativ 0,0658}$${\ displaystyle q}$

Definiție în termeni de funcții theta Neville

Funcțiile eliptice Jacobi pot fi definite foarte simplu folosind funcțiile theta Neville :

${\ displaystyle \ operatorname {pq} (u, m) = {\ frac {\ theta _ {\ operatorname {p}} (u, m)} {\ theta _ {\ operatorname {q}} (u, m) }}}$

Simplificările produselor complicate ale funcțiilor eliptice Jacobi sunt adesea ușurate folosind aceste identități.

Transformări Jacobi

Transformările imaginare Jacobi

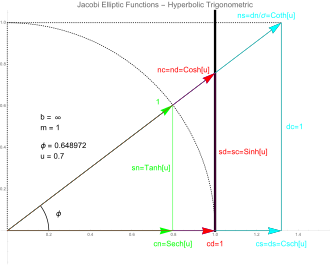
Graficul curbei degenerate Jacobi (x ² + y ² / b ² = 1, b = infinit) și cele douăsprezece funcții eliptice Jacobi pq (u, 1) pentru o anumită valoare a unghiului φ. Curba solidă este elipsa degenerată (x ² = 1) cu m = 1 și u = F (φ, 1) unde F (.,.) Este integrala eliptică de primul fel. Curba punctată este cercul unitar . Deoarece acestea sunt funcțiile Jacobi pentru m = 0 (funcții trigonometrice circulare), dar cu argumente imaginare, acestea corespund celor șase funcții trigonometrice hiperbolice.

Transformările imaginare Jacobi raportează diverse funcții ale variabilei imaginare iu sau, în mod echivalent, relații între diferite valori ale parametrului m . În ceea ce privește funcțiile majore:

${\ displaystyle \ operatorname {cn} (u, m) = \ operatorname {nc} (i \, u, 1 \! - \! m)}$

${\ displaystyle \ operatorname {sn} (u, m) = - i \ operatorname {sc} (i \, u, 1 \! - \! m)}$

${\ displaystyle \ operatorname {dn} (u, m) = \ operatorname {dc} (i \, u, 1 \! - \! m)}$

Folosind regula multiplicării, toate celelalte funcții pot fi exprimate în termenii celor trei de mai sus. Transformările pot fi , în general , scrise ca . Tabelul următor oferă pq ( u, m ) specificat. (Argumentele sunt suprimate) ${\ displaystyle \ operatorname {pq} (u, m) = \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(i \, u, 1 \! - \! m)}$${\ displaystyle \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(i \, u, 1 \! - \! m)}$${\ displaystyle (i \, u, 1 \! - \! m)}$

Jacobi Transformări imaginare ${\ displaystyle \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(i \, u, 1 \! - \! m)}$

		q
		c	s	n	d
p
	c	1	eu sunt	nc	nd
	s	-s sn	1	-este c	-i sd
	n	cn	eu cs	1	CD
	d	dn	eu sunt	DC	1

Deoarece funcțiile trigonometrice hiperbolice sunt proporționale cu funcțiile trigonometrice circulare cu argumente imaginare, rezultă că funcțiile Jacobi vor produce funcțiile hiperbolice pentru m = 1. În figură, curba Jacobi a degenerat la două linii verticale la x = 1 și x = -1.

Jacobi transformări reale

Transformările reale Jacobi dau expresii pentru funcțiile eliptice în termeni cu valori alternative de m . Transformările pot fi , în general , scrise ca . Tabelul următor oferă pq ( u, m ) specificat. (Argumentele sunt suprimate) ${\ displaystyle \ operatorname {pq} (u, m) = \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(k \, u, 1 / m)}$${\ displaystyle \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(k \, u, 1 / m)}$${\ displaystyle (k \, u, 1 / m)}$

Jacobi Transformări reale ${\ displaystyle \ gamma _ {\ operatorname {pq}} \ operatorname {pq} '(k \, u, 1 / m)}$

		q
		c	s	n	d
p
	c	1	${\ displaystyle k}$ ds	dn	DC
	s	${\ displaystyle {\ frac {1} {k}}}$ sd	1	${\ displaystyle {\ frac {1} {k}}}$ sn	${\ displaystyle {\ frac {1} {k}}}$ sc
	n	nd	${\ displaystyle k}$ ns	1	nc
	d	CD	${\ displaystyle k}$ cs	cn	1

Alte transformări Jacobi

Transformările reale și imaginare ale lui Jacobi pot fi combinate în diferite moduri pentru a produce încă trei transformări simple. Transformările reale și imaginare sunt două transformări într-un grup ( D ₃ sau grup anarmonic ) de șase transformări. Dacă

${\ displaystyle \ mu _ {R} (m) = 1 / m}$

este transformarea parametrului m în transformarea reală și

${\ displaystyle \ mu _ {I} (m) = 1-m = m '}$

este transformarea lui m în transformarea imaginară, apoi celelalte transformări pot fi construite prin aplicarea succesivă a acestor două transformări de bază, oferind doar încă trei posibilități:

${\ displaystyle {\ begin {align} \ mu _ {IR} (m) & = & \ mu _ {I} (\ mu _ {R} (m)) & = & - m '/ m \\\ mu _ {RI} (m) & = & \ mu _ {R} (\ mu _ {I} (m)) & = & 1 / m '\\\ mu _ {RIR} (m) & = & \ mu _ {R} (\ mu _ {I} (\ mu _ {R} (m))) & = & - m / m '\ end {align}}}$

Aceste cinci transformări, împreună cu transformarea identității (μ _U (m) = m) dau grupul de 6 elemente. În ceea ce privește funcțiile eliptice Jacobi, transformarea generală poate fi exprimată folosind doar trei funcții:

${\ displaystyle \ operatorname {cs} (u, m) = \ gamma _ {i} \ operatorname {cs '} (\ gamma _ {i} u, \ mu _ {i} (m))}$

${\ displaystyle \ operatorname {ns} (u, m) = \ gamma _ {i} \ operatorname {ns '} (\ gamma _ {i} u, \ mu _ {i} (m))}$

${\ displaystyle \ operatorname {ds} (u, m) = \ gamma _ {i} \ operatorname {ds '} (\ gamma _ {i} u, \ mu _ {i} (m))}$

unde i = U, I, IR, R, RI sau RIR, identificând transformarea, γ _i este un factor de multiplicare comun acestor trei funcții, iar primul indică funcția transformată. Celelalte nouă funcții transformate pot fi construite din cele trei de mai sus. Motivul pentru care funcțiile cs, ns, ds au fost alese pentru a reprezenta transformarea este că celelalte funcții vor fi rapoarte ale acestor trei (cu excepția inverselor lor) și factorii de multiplicare se vor anula.

Următorul tabel listează factorii de multiplicare pentru cele trei funcții ps, m transformate și numele funcțiilor transformate pentru fiecare dintre cele șase transformări. (Ca de obicei, k ² = m, 1-k ² = k ₁ ² = m 'și argumentele ( ) sunt suprimate) ${\ displaystyle \ gamma _ {i} u, \ mu _ {i} (m)}$

Parametrii pentru cele șase transformări

Transformarea i	${\ displaystyle \ gamma _ {i}}$	${\ displaystyle \ mu _ {i} (m)}$	cs '	ns '	ds '
U	1	m	cs	ns	ds
Eu	eu	eu	ns	cs	ds
IR	ik	-m '/ m	ds	cs	ns
R	k	1 / m	ds	ns	cs
RI	ik 1	1 / m '	ns	ds	cs
RIR	k 1	-m / m '	cs	ds	ns

Astfel, de exemplu, putem construi următorul tabel pentru transformarea RIR. Transformarea este în general scrisă (argumentele sunt suprimate) ${\ displaystyle \ operatorname {pq} (u, m) = \ gamma _ {\ operatorname {pq}} \, \ operatorname {pq '} (k' \, u, -m / m ')}$${\ displaystyle (k '\, u, -m / m')}$

Transformarea RIR ${\ displaystyle \ gamma _ {\ operatorname {pq}} \, \ operatorname {pq '} (k' \, u, -m / m ')}$

		q
		c	s	n	d
p
	c	1	k 'cs	CD	cn
	s	${\ displaystyle {\ frac {1} {k '}}}$ sc	1	${\ displaystyle {\ frac {1} {k '}}}$ sd	${\ displaystyle {\ frac {1} {k '}}}$ sn
	n	DC	${\ displaystyle k '}$ ds	1	dn
	d	nc	${\ displaystyle k '}$ ns	nd	1

Valoarea transformărilor Jacobi este că orice set de funcții eliptice Jacobi cu orice parametru complex m poate fi convertit într-un alt set pentru care 0 <= m <= 1 și, pentru valorile reale ale lui u , valorile funcției vor fi reale .

Hiperbola Jacobi

Graficul hiperbolei Jacobi ( x ² + y ² / b ² = 1, b imaginar) și cele douăsprezece funcții eliptice Jacobi pq (u, m) pentru valori particulare ale unghiului φ și parametrului b . Curba solidă este hiperbola, cu m = 1-1 / b ² și u = F (φ, m) unde F (.,.) Este integrala eliptică de primul fel. Curba punctată este cercul unitar. Pentru triunghiul ds-dc, σ = sin (φ) cos (φ) .

Introducând numere complexe, elipsa noastră are o hiperbolă asociată:

${\ displaystyle x ^ {2} - {\ frac {y ^ {2}} {b ^ {2}}} = 1}$

de la aplicarea transformării imaginare a lui Jacobi la funcțiile eliptice în ecuația de mai sus pentru x și  y .

${\ displaystyle x = {\ frac {1} {\ operatorname {dn} (u, 1-m)}}, \ quad y = {\ frac {\ operatorname {sn} (u, 1-m)} {\ operatorname {dn} (u, 1-m)}}}$

Rezultă că putem pune . Deci elipsa noastră are o elipsă duală cu m înlocuită cu 1-m. Acest lucru duce la torul complex menționat în Introducere. În general, m poate fi un număr complex, dar când m este real și m <0, curba este o elipsă cu axa majoră în direcția x. La m = 0 curba este un cerc, iar pentru 0 <m <1, curba este o elipsă cu axa majoră în direcția y. La m = 1, curba degenerează în două linii verticale la x = + / - 1. Pentru m> 1, curba este o hiperbolă. Când m este complex, dar nu real, x sau y sau ambele sunt complexe și curba nu poate fi descrisă pe o diagramă xy reală. ${\ displaystyle x = \ operatorname {dn} (u, 1-m), y = \ operatorname {sn} (u, 1-m)}$

Funcții minore

Inversarea ordinii celor două litere ale numelui funcției are ca rezultat reciprocitatea celor trei funcții de mai sus:

${\ displaystyle {\ begin {align} \ operatorname {ns} (u) = {\ frac {1} {\ operatorname {sn} (u)}}, \ qquad \ operatorname {nc} (u) = {\ frac {1} {\ operatorname {cn} (u)}}, \ qquad \ operatorname {nd} (u) = {\ frac {1} {\ operatorname {dn} (u)}}. \ End {align}} }$

În mod similar, raporturile celor trei funcții primare corespund primei litere a numărătorului urmată de prima literă a numitorului:

${\ displaystyle {\ begin {align} \ operatorname {sc} (u) = {\ frac {\ operatorname {sn} (u)} {\ operatorname {cn} (u)}}, \ qquad \ operatorname {sd} (u) = {\ frac {\ operatorname {sn} (u)} {\ operatorname {dn} (u)}}, \ qquad \ operatorname {dc} (u) = {\ frac {\ operatorname {dn} ( u)} {\ operatorname {cn} (u)}}, \ qquad \ operatorname {ds} (u) = {\ frac {\ operatorname {dn} (u)} {\ operatorname {sn} (u)}} , \ qquad \ operatorname {cs} (u) = {\ frac {\ operatorname {cn} (u)} {\ operatorname {sn} (u)}}, \ qquad \ operatorname {cd} (u) = {\ frac {\ operatorname {cn} (u)} {\ operatorname {dn} (u)}}. \ end {align}}}$

Mai compact, avem

${\ displaystyle \ operatorname {pq} (u) = {\ frac {\ operatorname {pn} (u)} {\ operatorname {qn} (u)}}}$

unde p și q sunt oricare dintre literele s, c, d.

Periodicitate, poli și reziduuri

Graficele fazei pentru cele douăsprezece funcții eliptice Jacobi pq (u, m) ca argument complex funcțional u, cu poli și zerouri indicați. Graficele sunt pe un ciclu complet în direcțiile reale și imaginare, cu porțiunea colorată care indică faza în funcție de roata de culoare din dreapta jos (care înlocuiește funcția dd banală). Regiunile cu amplitudine sub 1/3 sunt colorate în negru, indicând aproximativ locația unui zero, în timp ce regiunile cu amplitudine peste 3 sunt colorate în alb, indicând aproximativ poziția unui pol. Toate graficele folosesc m = 2/3 cu K = K (m), K '= K (1-m), K (.) Fiind integralul eliptic complet de primul fel. Săgețile către poli indică în direcția fazei zero. Săgețile dreapta și stânga implică reziduuri reale pozitive și, respectiv, negative. Săgețile în sus și în jos implică reziduuri imaginare pozitive și, respectiv, negative.

În planul complex al argumentului u , funcțiile eliptice Jacobi formează un model repetitiv de poli (și zerouri). Reziduurile polilor au toate aceeași amplitudine, diferind doar în semn. Fiecare funcție pq (u, m) are o funcție inversă qp (u, m) în care se schimbă pozițiile polilor și zero-urilor. Perioadele de repetare sunt în general diferite în direcțiile reale și imaginare, de unde utilizarea termenului „dublu periodic” pentru a le descrie.

Dubla periodicitate a funcțiilor eliptice Jacobi poate fi exprimată ca:

${\ displaystyle \ operatorname {pq} (u + 2 \ alpha K (m) + 2i \ beta K (1-m) \ ,, \, m) = (- 1) ^ {\ gamma} \ operatorname {pq} (u, m)}$

unde α și β sunt orice pereche de numere întregi. K (.) Este integrala eliptică completă de primul fel, cunoscută și sub numele de perioadă de sfert . Puterea unității negative (γ) este dată în tabelul următor:

${\ displaystyle \ gamma}$

		q
		c	s	n	d
p
	c	0	β	α + β	α
	s	β	0	α	α + β
	n	α + β	α	0	β
	d	α	α + β	β	0

Când factorul (-1) ^γ este egal cu -1, ecuația exprimă cvasi-periodicitate. Când este egal cu unitate, exprimă periodicitate deplină. Se poate observa, de exemplu, că pentru intrările care conțin doar α când α este egal, periodicitatea completă este exprimată prin ecuația de mai sus, iar funcția are perioade complete de 4K (m) și 2iK (1-m). La fel, funcțiile cu intrări care conțin doar β au perioade complete de 2K (m) și 4iK (1-m), în timp ce cele cu α + β au perioade complete de 4K (m) și 4iK (1-m).

În diagrama din dreapta, care trasează o unitate repetată pentru fiecare funcție, indicând faza împreună cu locația polilor și a zero-urilor, se pot nota o serie de regularități: inversul fiecărei funcții este opus diagonalei și are aceeași dimensiune celulă unitară, cu poli și zerouri schimbate. Aranjamentul polului și zero în dreptunghiul auxiliar format din (0,0), (K, 0), (0, K ') și (K, K') sunt în conformitate cu descrierea polului și poziționarea zero descrisă la introducerea de mai sus. De asemenea, dimensiunea ovalilor albi care indică poli sunt o măsură aproximativă a amplitudinii reziduului pentru acel pol. Reziduurile polilor cei mai apropiați de origine din figură (adică în dreptunghiul auxiliar) sunt enumerate în următorul tabel:

Reziduuri ale funcțiilor eliptice Jacobi

		q
		c	s	n	d
p
	c		1	${\ displaystyle - {\ frac {i} {k}}}$	${\ displaystyle - {\ frac {1} {k}}}$
	s	${\ displaystyle - {\ frac {1} {k '}}}$		${\ displaystyle {\ frac {1} {k}}}$	${\ displaystyle - {\ frac {i} {k \, k '}}}$
	n	${\ displaystyle - {\ frac {1} {k '}}}$	1		${\ displaystyle - {\ frac {i} {k '}}}$
	d	-1	1	${\ displaystyle -i}$

Atunci când este cazul, polii deplasați mai sus cu 2K sau deplasați spre dreapta cu 2K 'au aceeași valoare, dar cu semne inversate, în timp ce cei opuși în diagonală au aceeași valoare. Rețineți că polii și zero-urile de pe marginile stânga și inferioară sunt considerate parte a celulei unității, în timp ce cele de pe marginile superioare și dreapta nu sunt.

Relațiile dintre pătratele funcțiilor

Relațiile dintre pătratele funcțiilor pot fi derivate din două relații de bază (Argumente ( u , m ) suprimate):

${\ displaystyle \ operatorname {cn} ^ {2} + \ operatorname {sn} ^ {2} = 1}$

${\ displaystyle \ operatorname {cn} ^ {2} + m '\ operatorname {sn} ^ {2} = \ operatorname {dn} ^ {2}}$

unde m + m '  = 1 și m  =  k ² . Înmulțirea cu orice funcție a formei nq produce ecuații mai generale:

${\ displaystyle \ operatorname {cq} ^ {2} + \ operatorname {sq} ^ {2} = \ operatorname {nq} ^ {2}}$

${\ displaystyle \ operatorname {cq} ^ {2} + m '\ operatorname {sq} ^ {2} = \ operatorname {dq} ^ {2}}$

Cu q = d , acestea corespund trigonometic ecuațiilor pentru cercul unității ( ) și elipsa unității ( ), cu x = cd , y = sd și r = nd . Folosind regula multiplicării, pot fi derivate și alte relații. De exemplu: ${\ displaystyle x ^ {2} + y ^ {2} = r ^ {2}}$${\ displaystyle x ^ {2} + m'y ^ {2} = 1}$

${\ displaystyle - \ operatorname {dn} ^ {2} + m '= - m \ operatorname {cn} ^ {2} = m \ operatorname {sn} ^ {2} -m}$

${\ displaystyle -m '\ operatorname {nd} ^ {2} + m' = - mm '\ operatorname {sd} ^ {2} = m \ operatorname {cd} ^ {2} -m}$

${\ displaystyle m '\ operatorname {sc} ^ {2} + m' = m '\ operatorname {nc} ^ {2} = \ operatorname {dc} ^ {2} -m}$

${\ displaystyle \ operatorname {cs} ^ {2} + m '= \ operatorname {ds} ^ {2} = \ operatorname {ns} ^ {2} -m}$

Teoreme de adiție

Funcțiile satisfac cele două relații pătrate

${\ displaystyle \ operatorname {cn} ^ {2} (u, k) + \ operatorname {sn} ^ {2} (u, k) = 1, \,}$

${\ displaystyle \ operatorname {dn} ^ {2} (u, k) + k ^ {2} \ operatorname {sn} ^ {2} (u, k) = 1. \,}$

Din aceasta vedem că (cn, sn, dn) parametrizează o curbă eliptică care este intersecția celor două cvadrici definite de cele două ecuații de mai sus. Acum putem defini o lege de grup pentru punctele de pe această curbă prin formulele de adăugare pentru funcțiile Jacobi

${\ displaystyle {\ begin {align} \ operatorname {cn} (x + y) & = {\ operatorname {cn} (x) \ operatorname {cn} (y) - \ operatorname {sn} (x) \ operatorname { sn} (y) \ operatorname {dn} (x) \ operatorname {dn} (y) \ over {1-k ^ {2} \ operatorname {sn} ^ {2} (x) \ operatorname {sn} ^ { 2} (y)}}, \\ [8pt] \ operatorname {sn} (x + y) & = {\ operatorname {sn} (x) \ operatorname {cn} (y) \ operatorname {dn} (y) + \ operatorname {sn} (y) \ operatorname {cn} (x) \ operatorname {dn} (x) \ over {1-k ^ {2} \ operatorname {sn} ^ {2} (x) \ operatorname { sn} ^ {2} (y)}}, \\ [8pt] \ operatorname {dn} (x + y) & = {\ operatorname {dn} (x) \ operatorname {dn} (y) -k ^ { 2} \ operatorname {sn} (x) \ operatorname {sn} (y) \ operatorname {cn} (x) \ operatorname {cn} (y) \ over {1-k ^ {2} \ operatorname {sn} ^ {2} (x) \ operatorname {sn} ^ {2} (y)}}. \ End {align}}}$

Formulele cu unghi dublu pot fi derivate cu ușurință din ecuațiile de mai sus prin setarea x = y . Formulele pe jumătate de unghi sunt toate de formă:

${\ displaystyle \ operatorname {pq} ({\ tfrac {1} {2}} u, m) ^ {2} = f _ {\ mathrm {p}} / f _ {\ mathrm {q}}}$

Unde:

${\ displaystyle f _ {\ mathrm {c}} = \ operatorname {cn} (u, m) + \ operatorname {dn} (u, m)}$

${\ displaystyle f _ {\ mathrm {s}} = 1- \ operatorname {cn} (u, m)}$

${\ displaystyle f _ {\ mathrm {n}} = 1 + \ operatorname {dn} (u, m)}$

${\ displaystyle f _ {\ mathrm {d}} = (1+ \ operatorname {dn} (u, m)) - m (1- \ operatorname {cn} (u, m))}$

Valori speciale

Valori pentru înjumătățirea K:

${\ displaystyle \ operatorname {sn} \ left [{\ tfrac {1} {2}} K (k); k \ right] = {\ frac {1} {\ sqrt {1 + {\ sqrt {1-k ^ {2}}}}}}}}$și și${\ displaystyle \ operatorname {cn} \ left [{\ tfrac {1} {2}} K (k); k \ right] = {\ frac {\ sqrt [{4}] {1-k ^ {2} }} {\ sqrt {1 + {\ sqrt {1-k ^ {2}}}}}}}$${\ displaystyle \ operatorname {dn} \ left [{\ tfrac {1} {2}} K (k); k \ right] = {\ sqrt [{4}] {1-k ^ {2}}}}$

Valori pentru treimile K:

${\ displaystyle \ operatorname {sn} \ left [{\ frac {1} {3}} K \ left ({\ frac {x ^ {3}} {{\ sqrt {x ^ {6} +1}} + 1}} \ right); {\ frac {x ^ {3}} {{\ sqrt {x ^ {6} +1}} + 1}} \ right] = {\ frac {{\ sqrt {2 {\ sqrt {x ^ {4} -x ^ {2} +1}} - x ^ {2} +2}} + {\ sqrt {x ^ {2} +1}} - 1} {{\ sqrt {2 {\ sqrt {x ^ {4} -x ^ {2} +1}} - x ^ {2} +2}} + {\ sqrt {x ^ {2} +1}} + 1}}}$

Pentru a obține x ^ 3, trebuie să luați tangenta de două ori a arctangentei modulului.

De asemenea, această ecuație duce la valoarea sn a treia din K:

${\ displaystyle k ^ {2} s ^ {4} -2k ^ {2} s ^ {3} + 2s-1 = 0}$

${\ displaystyle s = \ operatorname {sn} \ left [{\ tfrac {1} {3}} K (k); k \ right]}$

Aceste ecuații duc la celelalte valori ale funcțiilor Jacobi:

${\ displaystyle \ operatorname {cn} \ left [{\ tfrac {2} {3}} K (k); k \ right] = 1- \ operatorname {sn} \ left [{\ tfrac {1} {3} } K (k); k \ dreapta]}$

${\ displaystyle \ operatorname {dn} \ left [{\ tfrac {2} {3}} K (k); k \ right] = 1 / \ operatorname {sn} \ left [{\ tfrac {1} {3} } K (k); k \ dreapta] -1}$

Valori pentru cincimi din K:

Următoarea ecuație are următoarea soluție:

${\ displaystyle 4k ^ {2} x ^ {6} + 8k ^ {2} x ^ {5} +2 (1-k ^ {2}) ^ {2} x- (1-k ^ {2}) ^ {2} = 0}$

${\ displaystyle x = {\ frac {1} {2}} - {\ frac {1} {2}} k ^ {2} \ operatorname {sn} \ left [{\ tfrac {2} {5}} K (k); k \ right] ^ {2} \ operatorname {sn} \ left [{\ tfrac {4} {5}} K (k); k \ right] ^ {2} = {\ frac {\ operatorname {sn} \ left [{\ frac {4} {5}} K (k); k \ right] ^ {2} - \ operatorname {sn} \ left [{\ frac {2} {5}} K ( k); k \ right] ^ {2}} {2 \ operatorname {sn} \ left [{\ frac {2} {5}} K (k); k \ right] \ operatorname {sn} \ left [{ \ frac {4} {5}} K (k); k \ right]}}}$

Pentru a obține valorile sn, trebuie să puneți soluția x în următoarele expresii:

${\ displaystyle {\ sqrt {k ^ {2} +1}} \ operatorname {sn} \ left [{\ tfrac {2} {5}} K (k); k \ right] = {\ sqrt {2 ( -x ^ {2} -x + 1) (x ^ {2} + 1-x {\ sqrt {x ^ {2} +1}})}}}$

${\ displaystyle {\ sqrt {k ^ {2} +1}} \ operatorname {sn} \ left [{\ tfrac {4} {5}} K (k); k \ right] = {\ sqrt {2 ( -x ^ {2} -x + 1) (x ^ {2} + 1 + x {\ sqrt {x ^ {2} +1}})}}}$

Extindere în termeni de nume

Să Nome să fie , , și lăsați . Apoi, funcțiile au expansiuni ca seria Lambert${\ displaystyle q = \ exp (- \ pi K '(k) / K (k)) = e ^ {i \ pi \ tau}}$${\ displaystyle \ operatorname {Im} (\ tau)> 0}$${\ displaystyle m = k ^ {2}}$${\ displaystyle v = \ pi u / (2K (k))}$

${\ displaystyle \ operatorname {sn} (u; k) = {\ frac {2 \ pi} {kK (k)}} \ sum _ {n = 0} ^ {\ infty} {\ frac {q ^ {n +1/2}} {1-q ^ {2n + 1}}} \ sin ((2n + 1) v),}$

${\ displaystyle \ operatorname {cn} (u; k) = {\ frac {2 \ pi} {kK (k)}} \ sum _ {n = 0} ^ {\ infty} {\ frac {q ^ {n +1/2}} {1 + q ^ {2n + 1}}} \ cos ((2n + 1) v),}$

${\ displaystyle \ operatorname {dn} (u; k) = {\ frac {\ pi} {2K (k)}} + {\ frac {2 \ pi} {K (k)}} \ sum _ {n = 1} ^ {\ infty} {\ frac {q ^ {n}} {1 + q ^ {2n}}} \ cos (2nv)}$

când . ${\ displaystyle q \ exp (2 | \ operatorname {Im} (v) |) <1}$

Funcțiile eliptice Jacobi ca soluții de ecuații diferențiale ordinare neliniare

La derivații celor trei funcții de bază eliptic Jacobi sunt:

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} z}} \ operatorname {sn} (z) = \ operatorname {cn} (z) \ operatorname {dn} (z),}$

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} z}} \ operatorname {cn} (z) = - \ operatorname {sn} (z) \ operatorname {dn} (z),}$

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} z}} \ operatorname {dn} (z) = - k ^ {2} \ operatorname {sn} (z) \ operatorname {cn} (z).}$

Acestea pot fi utilizate pentru a deriva derivatele tuturor celorlalte funcții așa cum se arată în tabelul de mai jos (argumentele (u, m) suprimate):

Derivate ${\ displaystyle {\ frac {d} {du}} \ operatorname {pq} (u, m)}$

		q
		c	s	n	d
p
	c	0	-ds ns	-dn sn	-md sd
	s	dc nc	0	cn dn	cd nd
	n	dc sc	-cs ds	0	m cd sd
	d	m 'nc sc	-cs ns	-m cn sn	0

Cu teoremele adunării de mai sus și pentru un k dat cu 0 <  k  <1, funcțiile majore sunt deci soluții la următoarele ecuații diferențiale ordinare neliniare :

• ${\ displaystyle \ operatorname {sn} (x)}$rezolvă ecuațiile diferențiale și${\ displaystyle {\ frac {\ mathrm {d} ^ {2} y} {\ mathrm {d} x ^ {2}}} + (1 + k ^ {2}) y-2k ^ {2} y ^ {3} = 0}$${\ displaystyle \ left ({\ frac {\ mathrm {d} y} {\ mathrm {d} x}} \ right) ^ {2} = (1-y ^ {2}) (1-k ^ {2 } y ^ {2})}$
• ${\ displaystyle \ operatorname {cn} (x)}$rezolvă ecuațiile diferențiale și${\ displaystyle {\ frac {\ mathrm {d} ^ {2} y} {\ mathrm {d} x ^ {2}}} + (1-2k ^ {2}) y + 2k ^ {2} y ^ {3} = 0}$${\ displaystyle \ left ({\ frac {\ mathrm {d} y} {\ mathrm {d} x}} \ right) ^ {2} = (1-y ^ {2}) (1-k ^ {2 } + k ^ {2} y ^ {2})}$
• ${\ displaystyle \ operatorname {dn} (x)}$rezolvă ecuațiile diferențiale și${\ displaystyle {\ frac {\ mathrm {d} ^ {2} y} {\ mathrm {d} x ^ {2}}} - (2-k ^ {2}) y + 2y ^ {3} = 0 }$${\ displaystyle \ left ({\ frac {\ mathrm {d} y} {\ mathrm {d} x}} \ right) ^ {2} = (y ^ {2} -1) (1-k ^ {2 } -y ^ {2})}$

Aproximare în ceea ce privește funcțiile hiperbolice

Funcțiile eliptice Jacobi pot fi extinse în ceea ce privește funcțiile hiperbolice. Când este aproape de unitate, astfel încât și puterile superioare ale pot fi neglijate, avem: ${\ displaystyle m}$${\ displaystyle m '^ {2}}$${\ displaystyle m '}$

• sn ( u ):
  $${\ displaystyle \ operatorname {sn} (u, m) \ approx \ tanh (u) + {\ frac {1} {4}} m '(\ sinh (u) \ cosh (u) -u) \ operatorname { sech} ^ {2} (u).}$$

  
• cn ( u ):
  $${\ displaystyle \ operatorname {cn} (u, m) \ approx \ operatorname {sech} (u) - {\ frac {1} {4}} m '(\ sinh (u) \ cosh (u) -u) \ tanh (u) \ operatorname {sech} (u).}$$

  
• dn ( u ):
  $${\ displaystyle \ operatorname {dn} (u, m) \ approx \ operatorname {sech} (u) + {\ frac {1} {4}} m '(\ sinh (u) \ cosh (u) + u) \ tanh (u) \ operatorname {sech} (u).}$$

  
• sunt ( u ):
  $${\ displaystyle \ operatorname {am} (u, m) \ approx \ operatorname {gd} (u) + {\ frac {1} {4}} m '(\ sinh (u) \ cosh (u) -u) \ operatorname {sech} (u).}$$

  

Fracții continuate

Presupunând numere reale cu și nome , cu modul eliptic . Dacă , unde este integralul eliptic complet de primul fel , atunci deține următoarea expansiune a fracției${\ displaystyle a, p}$${\ displaystyle 0 <a <p}$ ${\ displaystyle q = e ^ {\ pi i \ tau}}$${\ displaystyle \ operatorname {Im} (\ tau)> 0}$ ${\ textstyle k (\ tau) = {\ sqrt {1-k '(\ tau) ^ {2}}} = (\ vartheta _ {10} (0; \ tau) / \ vartheta _ {00} (0 ; \ tau)) ^ {2}}$${\ displaystyle K [\ tau] = K (k (\ tau))}$${\ displaystyle K (x) = \ pi / 2 \ cdot {} _ {2} F_ {1} (1 / 2,1 / 2; 1; x ^ {2})}$

${\ displaystyle {\ begin {align} & {\ frac {{\ textrm {dn}} \ left ((p / 2-a) \ tau K \ left [{\ frac {p \ tau} {2}} \ dreapta]; k \ left ({\ frac {p \ tau} {2}} \ right) \ right)} {\ sqrt {k '\ left ({\ frac {p \ tau} {2}} \ right) }}} = {\ frac {\ sum _ {n = - \ infty} ^ {\ infty} q ^ {p / 2n ^ {2} + (p / 2-a) n}} {\ sum _ {n = - \ infty} ^ {\ infty} (- 1) ^ {n} q ^ {p / 2n ^ {2} + (p / 2-a) n}}} \\ [4pt] = {} & - 1 + {\ frac {2} {1 -}} {\ frac {q ^ {a} + q ^ {pa}} {1-q ^ {p} +}} {\ frac {(q ^ {a} + q ^ {2p-a}) (q ^ {a + p} + q ^ {pa})} {1-q ^ {3p} +}} {\ frac {q ^ {p} (q ^ {a } + q ^ {3p-a}) (q ^ {a + 2p} + q ^ {pa})} {1-q ^ {5p} +}} {\ frac {q ^ {2p} (q ^ { a} + q ^ {4p-a}) (q ^ {a + 3p} + q ^ {pa})} {1-q ^ {7p} +}} \ ldots \ end {align}}}$