Logaritm - Logarithm

Graficele funcțiilor logaritmice, cu trei baze utilizate în mod obișnuit. Punctele speciale log _b  b = 1 sunt indicate prin linii punctate, iar toate curbele se intersectează în log _b  1 = 0 .

Operatii aritmetice v t e

Adăugare (+) ${\ displaystyle \ scriptstyle \ left. {\ begin {matrix} \ scriptstyle {\ text {term}} \, + \, {\ text {term}} \\\ scriptstyle {\ text {summand}} \, + \ , {\ text {summand}} \\\ scriptstyle {\ text {addend}} \, + \, {\ text {addend}} \\\ scriptstyle {\ text {augend}} \, + \, {\ text {addend}} \ end {matrix}} \ right \} \, = \,}$ ${\ displaystyle \ scriptstyle {\ text {sum}}}$ Scădere (-) ${\ displaystyle \ scriptstyle \ left. {\ begin {matrix} \ scriptstyle {\ text {term}} \, - \, {\ text {term}} \\\ scriptstyle {\ text {minuend}} \, - \ , {\ text {subtrahend}} \ end {matrix}} \ right \} \, = \,}$ ${\ displaystyle \ scriptstyle {\ text {difference}}}$ Înmulțirea (×) ${\ displaystyle \ scriptstyle \ left. {\ begin {matrix} \ scriptstyle {\ text {factor}} \, \ times \, {\ text {factor}} \\\ scriptstyle {\ text {multiplier}} \, \ ori \, {\ text {multiplicand}} \ end {matrix}} \ right \} \, = \,}$ ${\ displaystyle \ scriptstyle {\ text {product}}}$ Divizie (÷) ${\ displaystyle \ scriptstyle \ left. {\ begin {matrix} \ scriptstyle {\ frac {\ scriptstyle {\ text {dividend}}} {\ scriptstyle {\ text {divisor}}}} \\\ scriptstyle {\ text { }} \\\ scriptstyle {\ frac {\ scriptstyle {\ text {numerator}}} {\ scriptstyle {\ text {denominator}}}} \ end {matrix}} \ right \} \, = \,}$ ${\ displaystyle {\ begin {matrix} \ scriptstyle {\ text {fraction}} \\\ scriptstyle {\ text {quotient}} \\\ scriptstyle {\ text {ratio}} \ end {matrix}}}$ Exponențierea ${\ displaystyle \ scriptstyle {\ text {base}} ^ {\ text {exponent}} \, = \,}$ ${\ displaystyle \ scriptstyle {\ text {power}}}$ a n- a rădăcină (√) ${\ displaystyle \ scriptstyle {\ sqrt [{\ text {degree}}] {\ scriptstyle {\ text {radicand}}}} \, = \,}$ ${\ displaystyle \ scriptstyle {\ text {root}}}$ Logaritm (jurnal) ${\ displaystyle \ scriptstyle \ log _ {\ text {base}} ({\ text {anti-logaritm}}) \, = \,}$ ${\ displaystyle \ scriptstyle {\ text {logaritm}}}$

În matematică , logaritmul este funcția inversă a exponențierii . Asta înseamnă că logaritmul unui număr dat  x este exponentul la care trebuie ridicat un alt număr fix, baza  b , pentru a produce acel număr  x . În cel mai simplu caz, logaritmul numără numărul de apariții ale aceluiași factor în multiplicare repetată; de exemplu, din moment ce 1000 = 10 × 10 × 10 = 10 ³ , „baza logaritmică 10” din 1000 este 3, sau log ₁₀  (1000) = 3 . Logaritmul lui x la baza  b este notat ca log _b  ( x ) sau fără paranteze, log _b  x sau chiar fără baza explicită, log  x , când nu este posibilă confuzie sau când baza nu contează, cum ar fi în notație O mare .

Mai general, exponențierea permite ca orice număr real pozitiv ca bază să fie ridicat la orice putere reală, producând întotdeauna un rezultat pozitiv, deci log _b ( x ) pentru oricare două numere reale pozitive  b și  x , unde  b nu este egal cu  1 , este întotdeauna un număr real unic  y . Mai explicit, relația definitorie dintre exponențiere și logaritm este:

${\ displaystyle \ log _ {b} (x) = y \}$exact dacă și și și .${\ displaystyle \ b ^ {y} = x \}$${\ displaystyle \ x> 0}$${\ displaystyle \ b> 0}$${\ displaystyle \ b \ neq 1}$

De exemplu, jurnal ₂  64 = 6 , ca 2 ⁶ = 64 .

Baza de logaritm 10 (adică b = 10 ) se numește logaritm zecimal sau comun și este frecvent utilizată în știință și inginerie. Logaritmul natural are numarul  e (adică b ≈ 2,718 ) ca bază; utilizarea sa este răspândită în matematică și fizică , datorită integralei și derivatei sale mai simple . Cele binare logaritmi Utilizările fundamenteze 2 (adică b = 2 ) și este utilizat frecvent în informatică .

Logaritmii au fost introduși de John Napier în 1614 ca mijloc de simplificare a calculelor. Au fost adoptate rapid de navigatori, oameni de știință, ingineri, topografi și alții pentru a efectua calcule de înaltă precizie mai ușor. Folosind tabele logaritmice , pașii obosiți de multiplicare cu mai multe cifre pot fi înlocuiți cu căutări de tabel și adăugare mai simplă. Acest lucru este posibil datorită faptului - important în sine - că logaritmul unui produs este suma logaritmilor factorilor:

${\ displaystyle \ log _ {b} (xy) = \ log _ {b} x + \ log _ {b} y,}$

cu condiția ca b , x și y să fie toate pozitive și b ≠ 1 . Regula de diapozitive , de asemenea , bazat pe logaritmi, permite calcule rapide fara tabele, dar la o precizie mai mică. Noțiunea actuală de logaritmi vine de la Leonhard Euler , care i-a conectat la funcția exponențială în secolul al XVIII-lea și care a introdus și litera e ca bază a logaritmilor naturali.

Cântarele logaritmice reduc cantități mari la sfere mici. De exemplu, decibelul (dB) este o unitate utilizată pentru a exprima raportul ca logaritmi , în special pentru puterea și amplitudinea semnalului (din care presiunea sonoră este un exemplu obișnuit). În chimie, pH-ul este o măsură logaritmică a acidității unei soluții apoase . Logaritmii sunt banali în formulele științifice și în măsurătorile complexității algoritmilor și a obiectelor geometrice numite fractali . Ele ajută la descrierea raporturilor de frecvență ale intervalelor muzicale , apar în formule de numărare a numerelor prime sau aproximarea factorialelor , informează unele modele în psihofizică și pot ajuta în contabilitatea criminalistică .

În același mod în care logaritmul inversează exponențierea , logaritmul complex este funcția inversă a funcției exponențiale, indiferent dacă este aplicată numerelor reale sau numerelor complexe . Logaritmul discret modular este o altă variantă; are utilizări în criptografia cu cheie publică .

Motivație și definiție

Graficul bazei logaritmului 2 traversează x -axis la x = 1 și trece prin punctele (2, 1) , (4, 2) și (8, 3) , ilustrând, de exemplu, log ₂ (8) = 3 și 2 ³ = 8 . Graficul se apropie în mod arbitrar de axa- y , dar nu îl îndeplinește .

Adunarea , multiplicarea și exponențierea sunt trei dintre cele mai fundamentale operații aritmetice. Adunarea, cea mai simplă dintre acestea, este anulată prin scădere: când adăugați 5 la x pentru a obține x + 5 , pentru a inversa această operație, trebuie să scădeți 5 din x + 5 . Înmulțirea, cea mai simplă operație următoare, este anulată prin împărțire : dacă înmulțiți x cu 5 pentru a obține 5 x , puteți împărți 5 x cu 5 pentru a reveni la expresia originală x . Logaritmii anulează, de asemenea, o operație aritmetică fundamentală, exponențierea. Exponențierea este atunci când ridicați un număr la o anumită putere. De exemplu, creșterea 2 la puterea 3 este egală cu 8 :

${\ displaystyle 2 ^ {3} = 2 \ times 2 \ times 2 = 8}$

Cazul general este atunci când ridicați un număr  b la puterea lui y pentru a obține x :

${\ displaystyle b ^ {y} = x}$

Numărul  b este denumit baza acestei expresii. Baza este numărul crescut la o anumită putere - în exemplul de mai sus, baza expresiei 2 ³ = 8 este 2 . Este ușor să faceți din bază subiectul expresiei: tot ce trebuie să faceți este să luați rădăcina a y - a ambelor părți. Asta da

${\ displaystyle b = {\ sqrt [{y}] {x}}.}$

Este mai puțin ușor de a face y subiectul expresiei. Logaritmii ne permit să facem acest lucru:

${\ displaystyle y = \ log _ {b} x.}$

Această expresie înseamnă că y este egal cu puterea la care ați crește b , pentru a obține x . Această operație anulează exponențierea, deoarece logaritmul lui x vă spune exponentul la care baza a fost ridicată.

Exponențierea

Această subsecțiune conține o scurtă prezentare generală a operației de exponențiere, care este fundamentală pentru înțelegerea logaritmilor. Creșterea lui b la puterea n - a, unde n este un număr natural , se face înmulțind n  factori egali cu b . Puterea n - a lui b este scrisă b ⁿ , astfel încât

${\ displaystyle b ^ {n} = \ underbrace {b \ times b \ times \ cdots \ times b} _ {n {\ text {factors}}}.}$

Exponențierea poate fi extinsă la b ^y , unde b este un număr pozitiv și exponentul y este orice număr real . De exemplu, b ^-1 este reciprocul lui b , adică 1 / b . Creșterea lui b la puterea  1/2 este rădăcina pătrată a lui b .

Mai general, ridicarea lui b la o putere  rațională p / q , unde p și q sunt întregi, este dată de

${\ displaystyle b ^ {p / q} = {\ sqrt [{q}] {b ^ {p}}},}$

q rădăcina a -lea b ^p .

În cele din urmă, orice număr irațional (un număr real care nu este rațional) y poate fi aproximat la precizie arbitrară prin numere raționale. Acest lucru poate fi folosit pentru a calcula y puterea a -lea b : de exemplu , și este tot mai bine aproximată prin b ¹ , b ^1.4 , b ^1,41 , b ^1.414 , ... . O explicație mai detaliată, precum și formula b ^{m + n} = b ^m · b ⁿ este conținută în articolul despre exponențiere . ${\ displaystyle {\ sqrt {2}} \ approx 1.414 ...}$${\ displaystyle b ^ {\ sqrt {2}}}$

Definiție

Logaritmul unui număr real pozitiv x în raport cu baza  b este exponentul prin care b trebuie ridicate pentru a produce x . Cu alte cuvinte, logaritmul lui x la baza  b este soluția  y la ecuație

${\ displaystyle b ^ {y} = x.}$

Logaritmul este notată „ log _b  x “ (pronunțat ca „logaritmului x la bază  b “, „ a baza- b logaritmul x “, sau cel mai frecvent „log, de bază  b , din x “).

În ecuația y = log _b  x , valoarea  y este răspunsul la întrebarea „La ce putere trebuie crescută b , pentru a produce x ?”.

Exemple

• log ₂  16 = 4 , deoarece 2 ⁴ = 2 × 2 × 2 × 2 = 16 .
• Logaritmii pot fi și ei negativi: din moment ce${\ textstyle \ log _ {2} \! {\ frac {1} {2}} = - 1}$${\ textstyle 2 ^ {- 1} = {\ frac {1} {2 ^ {1}}} = {\ frac {1} {2}}.}$
• log ₁₀  150 este aproximativ 2,176, care se află între 2 și 3, la fel cum 150 se află între 10 ² = 100 și 10 ³ = 1000 .
• Pentru orice bază  b , log _b  b = 1 și log _b  1 = 0 , deoarece b ¹ = b și respectiv b ⁰ = 1 .

Identități logaritmice

Câteva formule importante, uneori numite identități logaritmice sau legi logaritmice , leagă logaritmii între ei.

Produs, coeficient, putere și rădăcină

Logaritmul unui produs este suma logaritmilor numerelor înmulțite; logaritmul raportului a două numere este diferența dintre logaritmi. Logaritmul puterii p -a unui număr este de p  ori logaritmul numărului în sine; logaritmul unei rădăcini p -a este logaritmul numărului împărțit la p . Tabelul următor listează aceste identități cu exemple. Fiecare dintre identități poate fi derivată după înlocuirea definițiilor logaritmului sau în partea stângă. ${\ displaystyle x = b ^ {\, \ log _ {b} x}}$${\ displaystyle y = b ^ {\, \ log _ {b} y}}$

	Formulă	Exemplu
Produs	${\ textstyle \ log _ {b} (xy) = \ log _ {b} x + \ log _ {b} y}$	${\ textstyle \ log _ {3} 243 = \ log _ {3} (9 \ cdot 27) = \ log _ {3} 9+ \ log _ {3} 27 = 2 + 3 = 5}$
Coeficient	${\ textstyle \ log _ {b} \! {\ frac {x} {y}} = \ log _ {b} x- \ log _ {b} y}$	${\ textstyle \ log _ {2} 16 = \ log _ {2} \! {\ frac {64} {4}} = \ log _ {2} 64- \ log _ {2} 4 = 6-2 = 4}$
Putere	${\ textstyle \ log _ {b} \ left (x ^ {p} \ right) = p \ log _ {b} x}$	${\ textstyle \ log _ {2} 64 = \ log _ {2} \ left (2 ^ {6} \ right) = 6 \ log _ {2} 2 = 6}$
Rădăcină	${\ textstyle \ log _ {b} {\ sqrt [{p}] {x}} = {\ frac {\ log _ {b} x} {p}}}$	${\ textstyle \ log _ {10} {\ sqrt {1000}} = {\ frac {1} {2}} \ log _ {10} 1000 = {\ frac {3} {2}} = 1.5}$

Schimbarea bazei

Logaritmul log _b  x poate fi calculat din logaritmii lui x și b față de o bază arbitrară  k folosind următoarea formulă:

${\ displaystyle \ log _ {b} x = {\ frac {\ log _ {k} x} {\ log _ {k} b}}. \,$

Calculatoarele științifice tipice calculează logaritmii la bazele 10 și e . Logaritmii cu privire la orice bază  b pot fi determinați folosind oricare dintre acești doi logaritmi prin formula anterioară:

${\ displaystyle \ log _ {b} x = {\ frac {\ log _ {10} x} {\ log _ {10} b}} = {\ frac {\ log _ {e} x} {\ log _ {e} b}}.}$

Având în vedere un număr x și logaritmul său y = log _b  x la o bază necunoscută  b , baza este dată de:

${\ displaystyle b = x ^ {\ frac {1} {y}},}$

care poate fi văzut de la luarea ecuației definitorii la puterea lui${\ displaystyle x = b ^ {\, \ log _ {b} x} = b ^ {y}}$${\ displaystyle {\ tfrac {1} {y}}.}$

Bazele particulare

Parcele de logaritm pentru bazele 0,5, 2 și e

Dintre toate opțiunile pentru bază, trei sunt deosebit de frecvente. Acestea sunt b = 10 , b = e ( constanta matematică irațională ≈ 2.71828) și b = 2 ( logaritmul binar ). În analiza matematică , baza logaritmului e este larg răspândită datorită proprietăților analitice explicate mai jos. Pe de altă parte, logaritmii de bază-10 sunt ușor de utilizat pentru calculele manuale în sistemul numeric zecimal :

${\ displaystyle \ log _ {10} (10x) = \ log _ {10} 10+ \ log _ {10} x = 1 + \ log _ {10} x. \}$

Astfel, log ₁₀  ( x ) este legat de numărul de cifre zecimale ale unui întreg pozitiv x : numărul de cifre este cel mai mic întreg strict mai mare decât log ₁₀  ( x ) . De exemplu, jurnalul ₁₀ (1430) este aproximativ 3,15. Următorul număr întreg este 4, care este numărul de cifre din 1430. Atât logaritmul natural, cât și logaritmul de la baza a două sunt utilizate în teoria informației , corespunzând utilizării naturilor sau a biților ca unități fundamentale de informație, respectiv. Logaritmii binari sunt folosiți și în informatică , unde sistemul binar este omniprezent; în teoria muzicii , unde un raport de înălțime de două ( octava ) este omniprezent, iar centul este logaritmul binar (scalat cu 1200) al raportului dintre două tonuri adiacente cu temperaturi egale în muzica clasică europeană ; și în fotografie pentru a măsura valorile expunerii .

Următorul tabel listează notațiile comune pentru logaritmi la aceste baze și câmpurile în care sunt utilizate. Multe discipline scriu log  x în loc de log _b  x , când baza intenționată poate fi determinată din context. Apare și notația ^b log  x . Coloana „ Notare ISO” listează denumirile sugerate de Organizația Internațională pentru Standardizare ( ISO 80000-2 ). Deoarece jurnalul de notare x a fost utilizat pentru toate cele trei baze (sau când baza este nedeterminată sau imaterială), baza intenționată trebuie deseori dedusă pe baza contextului sau disciplinei. În informatică, jurnalul se referă de obicei la jurnalul ₂ , iar în matematică jurnalul se referă de obicei la jurnalul _e . În alte contexte, log înseamnă adesea log ₁₀ .

Istorie

Istoria logaritmi în secolul al XVII-Europa este descoperirea unei noi funcții , care a extins domeniul de analiză dincolo de domeniul de aplicare a metodelor algebrice. Metoda logaritmilor a fost propusă public de John Napier în 1614, într-o carte intitulată Mirifici Logarithmorum Canonis Descriptio ( Descrierea minunatei reguli a logaritmilor ). Înainte de invenția lui Napier, au existat alte tehnici cu scopuri similare, cum ar fi prostafareza sau utilizarea tabelelor de progresii, dezvoltate pe larg de Jost Bürgi în jurul anului 1600. Napier a inventat termenul pentru logaritm în latina mijlocie, „logaritmus”, derivat din greaca, care înseamnă literalmente „raport-număr”, din logos „proporție, raport, cuvânt” + aritmos „număr”.

Comun Logaritmul unui număr este indicele de acea putere de zece , care este egal cu numărul. A vorbi despre un număr care necesită atât de multe cifre este o aluzie aproximativă la logaritmul comun și a fost menționat de Arhimede ca „ordinea unui număr”. Primii logaritmi reali au fost metode euristice pentru a transforma multiplicarea în adunare, facilitând astfel calculul rapid. Unele dintre aceste metode au folosit tabele derivate din identități trigonometrice. Astfel de metode se numesc prostafareză .

Invenția funcției acum cunoscută sub numele de logaritm natural a început ca o încercare de a efectua o cuadratură a unei hiperbole dreptunghiulare de către Grégoire de Saint-Vincent , un iezuit belgian care locuiește la Praga. Arhimede scrisese Cadratura parabolei în secolul al III-lea î.Hr., dar o cvadratură pentru hiperbolă a evitat toate eforturile până când Saint-Vincent și-a publicat rezultatele în 1647. Relația pe care logaritmul o oferă între o progresie geometrică a argumentului său și o progresie aritmetică de valori, l-a determinat pe AA de Sarasa să facă legătura dintre cvadratura Saint-Vincent și tradiția logaritmilor în prostafareză , conducând la termenul „logaritm hiperbolic”, un sinonim pentru logaritm natural. În curând, noua funcție a fost apreciată de Christiaan Huygens și James Gregory . Notația Log y a fost adoptată de Leibniz în 1675, iar în anul următor a conectat-o ​​la integrală ${\ textstyle \ int {\ frac {dy} {y}}.}$

Înainte ca Euler să-și dezvolte concepția modernă despre logaritmi naturali complecși, Roger Cotes a avut un rezultat aproape echivalent când a arătat în 1714 că

${\ displaystyle \ log (\ cos \ theta + i \ sin \ theta) = i \ theta}$.

Tabelele logaritmice, regulile de diapozitive și aplicațiile istorice

Explicația Logaritmilor din Encyclopædia Britannica din 1797

Prin simplificarea calculelor dificile înainte ca calculatoarele și computerele să devină disponibile, logaritmii au contribuit la progresul științei, în special al astronomiei . Au fost esențiale pentru progresele în topografie , navigație cerească și alte domenii. Pierre-Simon Laplace numea logaritmi

„... [un] artificiu admirabil care, prin reducerea la câteva zile a muncii de mai multe luni, dublează viața astronomului și îi scutește de erorile și dezgustul inseparabile de calculele lungi.”

Deoarece funcția f ( x ) = b ^x este funcția inversă a log _b  x , a fost numită antilogaritm . În zilele noastre, această funcție este mai frecvent numită funcție exponențială .

Tabele jurnal

Un instrument cheie care a permis utilizarea practică a logaritmilor a fost tabelul logaritmilor . Primul astfel de tabel a fost compilat de Henry Briggs în 1617, imediat după invenția lui Napier, dar cu inovația utilizării a 10 ca bază. Primul tabel al lui Briggs conținea logaritmele comune ale tuturor numerelor întregi cuprinse între 1 și 1000, cu o precizie de 14 cifre. Ulterior, au fost scrise tabele cu un domeniu de aplicare în creștere. Aceste tabele enumeră valorile jurnalului ₁₀  x pentru orice număr  x dintr-un anumit interval, la o anumită precizie. Logaritmii de bază-10 au fost folosiți universal pentru calcul, de unde și denumirea de logaritm comun, deoarece numerele care diferă prin factori de 10 au logaritmi care diferă prin numere întregi. Logaritmul comun al lui x poate fi separat într-o parte întreagă și o parte fracționată , cunoscută sub numele de caracteristică și mantisă . Tabelele de logaritmi trebuie să includă doar mantisa, deoarece caracteristica poate fi ușor determinată prin numărarea cifrelor din punctul zecimal. Caracteristica lui 10 · x este una plus caracteristica lui x , iar mantisele lor sunt aceleași. Astfel, folosind un tabel de jurnal din trei cifre, logaritmul lui 3542 este aproximat cu

${\ displaystyle \ log _ {10} 3542 = \ log _ {10} (1000 \ cdot 3.542) = 3 + \ log _ {10} 3.542 \ approx 3+ \ log _ {10} 3.54 \,}$

O precizie mai mare poate fi obținută prin interpolare :

${\ displaystyle \ log _ {10} 3542 \ approx 3+ \ log _ {10} 3,54 + 0,2 (\ log _ {10} 3,55- \ log _ {10} 3,54) \,}$

Valoarea de 10 ^x poate fi determinată prin căutarea inversă în același tabel, deoarece logaritmul este o funcție monotonă .

Calcule

Produsul și coeficientul a două numere pozitive c și d au fost calculate în mod obișnuit ca suma și diferența logaritmilor lor. Produsul  cd sau coeficientul  c / d provine din căutarea antilogaritmului sumei sau diferenței, prin același tabel:

${\ displaystyle cd = 10 ^ {\, \ log _ {10} c} \, 10 ^ {\, \ log _ {10} d} = 10 ^ {\, \ log _ {10} c \, + \ , \ log _ {10} d}}$

și

${\ displaystyle {\ frac {c} {d}} = cd ^ {- 1} = 10 ^ {\, \ log _ {10} c \, - \, \ log _ {10} d}.}$

Pentru calculele manuale care necesită orice precizie apreciabilă, efectuarea căutărilor celor două logaritmi, calcularea sumei sau diferenței acestora și căutarea antilogaritmului este mult mai rapidă decât efectuarea înmulțirii prin metode anterioare, cum ar fi prostafareza , care se bazează pe identități trigonometrice .

Calculele puterilor și rădăcinilor sunt reduse la multiplicări sau diviziuni și căutări de către

${\ displaystyle c ^ {d} = \ left (10 ^ {\, \ log _ {10} c} \ right) ^ {d} = 10 ^ {\, d \ log _ {10} c}}$

și

${\ displaystyle {\ sqrt [{d}] {c}} = c ^ {\ frac {1} {d}} = 10 ^ {{\ frac {1} {d}} \ log _ {10} c} .}$

Calculele trigonometrice au fost facilitate de tabele care conțineau logaritmele comune ale funcțiilor trigonometrice .

Regulile de diapozitive

O altă aplicație critică a fost regula diapozitivului , o pereche de scale împărțite logaritmic utilizate pentru calcul. Scara logaritmică care nu alunecă, regula lui Gunter , a fost inventată la scurt timp după invenția lui Napier. William Oughtred a îmbunătățit-o pentru a crea regula de diapozitive - o pereche de cântare logaritmice mobile una față de cealaltă. Numerele sunt plasate pe cântare glisante la distanțe proporționale cu diferențele dintre logaritmii lor. Glisarea scării superioare echivalează cu adăugarea mecanică de logaritmi, așa cum este ilustrat aici:

Reprezentarea schematică a unei reguli de diapozitive. Începând de la 2 pe scara inferioară, adăugați distanța la 3 pe scara superioară pentru a ajunge la produsul 6. Regula diapozitivului funcționează deoarece este marcată astfel încât distanța de la 1 la x să fie proporțională cu logaritmul lui x .

De exemplu, adăugarea distanței de la 1 la 2 pe scara inferioară la distanța de la 1 la 3 pe scara superioară dă un produs de 6, care este citit în partea inferioară. Regula de diapozitive a fost un instrument esențial de calcul pentru ingineri și oameni de știință până în anii 1970, deoarece permite, în detrimentul preciziei, un calcul mult mai rapid decât tehnicile bazate pe tabele.

Proprietăți analitice

Un studiu mai profund al logaritmilor necesită conceptul unei funcții . O funcție este o regulă care, dat fiind un număr, produce un alt număr. Un exemplu este funcția care produce puterea x -a lui b din orice număr real  x , unde baza  b este un număr fix. Această funcție este scrisă: f ( x ) = b ^x .

Funcția logaritmică

Pentru a justifica definiția logaritmilor, este necesar să arătăm că ecuația

${\ displaystyle b ^ {x} = y}$

are o soluție x și că această soluție este unică, cu condiția ca y să fie pozitiv și că b este pozitiv și inegal la 1. O dovadă a acestui fapt necesită teorema valorii intermediare din calculul elementar . Această teoremă afirmă că o funcție continuă care produce două valori m și n produce, de asemenea, orice valoare care se află între m și n . O funcție este continuă dacă nu „sare”, adică dacă graficul său poate fi desenat fără a ridica stiloul.

Se poate arăta că această proprietate este valabilă pentru funcția f ( x ) = b ^x . Deoarece f ia valori pozitive arbitrar mari și arbitrar mici, orice număr y > 0 se află între f ( x ₀ ) și f ( x ₁ ) pentru x ₀ și x ₁ adecvate . Prin urmare, teorema valorii intermediare asigură că ecuația f ( x ) = y are o soluție. Mai mult, există o singură soluție la această ecuație, deoarece funcția  f este strict crescătoare (pentru b > 1 ), sau strict descrescătoare (pentru 0 < b <1 ).

Soluția unică x este logaritmul lui y la baza  b , log _b  y . Funcția care atribuie lui y logaritmul său se numește funcție logaritmică sau funcție logaritmică (sau doar logaritm ).

Funcția log _b  x este caracterizată în esență de formula produsului

${\ displaystyle \ log _ {b} (xy) = \ log _ {b} x + \ log _ {b} y.}$

Mai precis, logaritmul către orice bază b > 1 este singura funcție crescătoare f de la realele pozitive la realele care satisfac f ( b ) = 1 și

${\ displaystyle f (xy) = f (x) + f (y).}$

Funcție inversă

Graficul logaritmului funcției log _b  ( x ) (albastru) se obține reflectând graficul funcției b ^x (roșu) la linia diagonală ( x = y ).

Formula logaritmului unei puteri spune în special că pentru orice număr  x ,

${\ displaystyle \ log _ {b} \ left (b ^ {x} \ right) = x \ log _ {b} b = x.}$

În proză, luând puterea x -a lui b și apoi logaritmul de bază- b dă înapoi x . Dimpotrivă, având în vedere un număr pozitiv  y , formula

${\ displaystyle b ^ {\ log _ {b} y} = y}$

spune că luând mai întâi logaritmul și apoi exponențierea dă înapoi y . Astfel, cele două modalități posibile de a combina (sau compune ) logaritmi și exponențiere redau numărul original. Prin urmare, logaritmul bazei  b este funcția inversă a lui f ( x ) = b ^x .

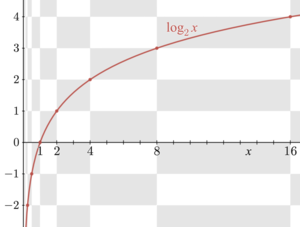
Funcțiile inverse sunt strâns legate de funcțiile originale. Graficele lor corespund reciproc la schimbul coordonatelor x - și y (sau la reflectarea la dreapta diagonală x = y ), așa cum se arată în dreapta: un punct ( t , u = b ^t ) pe graficul lui f dă un punct ( u , t = log _b  u ) pe graficul logaritmului și invers. În consecință, log _b  ( x ) divergă la infinit (devine mai mare decât orice număr dat) dacă x crește la infinit, cu condiția ca b să fie mai mare decât unul. În acest caz, log _b ( x ) este o funcție în creștere . Pentru b <1 , log _b  ( x ) tinde spre minus infinit în schimb. Când x se apropie de zero, log _b  x merge la minus infinit pentru b > 1 (plus infinit pentru b <1 , respectiv).

Derivat și antiderivat

Graficul logaritmului natural (verde) și al tangentei sale la x = 1,5 (negru)

Proprietățile analitice ale funcțiilor trec la inversele lor. Astfel, deoarece f ( x ) = b ^x este o funcție continuă și diferențiată , la fel este log _b  y . Aproximativ, o funcție continuă este diferențiată dacă graficul său nu are „colțuri” ascuțite. Mai mult, deoarece derivata lui f ( x ) se evaluează la ln ( b ) b ^x prin proprietățile funcției exponențiale , regula lanțului implică faptul că derivata lui log _b  x este dată de

${\ displaystyle {\ frac {d} {dx}} \ log _ {b} x = {\ frac {1} {x \ ln b}}.}$

Aceasta este, partia a tangentei atinge graficul baza- b logaritmul în punctul ( x , log _b  ( x )) este egal cu 1 / ( x  ln ( b )) .

Derivata lui ln ( x ) este 1 / x ; aceasta implică faptul că ln ( x ) este antiderivativul unic al 1 / x care are valoarea 0 pentru x = 1 . Această formulă foarte simplă a motivat calificarea ca „natural” logaritmul natural; acesta este și unul dintre principalele motive ale importanței constantei  e .

Derivata cu un argument funcțional generalizat f ( x ) este

${\ displaystyle {\ frac {d} {dx}} \ ln f (x) = {\ frac {f '(x)} {f (x)}}.}$

Cocientul din partea dreaptă se numește derivată logaritmică a lui f . Calculul f ' ( x ) prin intermediul derivatei lui l ( f ( x )) este cunoscut sub numele de diferențiere logaritmică . Antiderivativul logaritmului natural ln ( x ) este:

${\ displaystyle \ int \ ln (x) \, dx = x \ ln (x) -x + C.}$

Formulele conexe , cum ar fi antiderivatele logaritmilor la alte baze pot fi derivate din această ecuație folosind schimbarea bazelor.

Reprezentarea integrală a logaritmului natural

Logaritmul natural al t este zona umbrită de sub graficul funcției f ( x ) = 1 / x (reciprocă x ).

Logaritmul natural al t poate fi definită ca integrala definită :

${\ displaystyle \ ln t = \ int _ {1} ^ {t} {\ frac {1} {x}} \, dx.}$

Această definiție are avantajul că nu se bazează pe funcția exponențială sau orice funcție trigonometrică; definiția este în termenii unei integrale a unui simplu reciproc. Ca o integrală, ln ( t ) este egal cu aria dintre x -axa și graficul funcției 1 / x , variind de la x = 1 la x = t . Aceasta este o consecință a teoremei fundamentale a calculului și a faptului că derivata lui ln ( x ) este 1 / x . Formulele logaritmice ale produsului și puterii pot fi derivate din această definiție. De exemplu, formula produsului ln ( tu ) = ln ( t ) + ln ( u ) se deduce ca:

${\ displaystyle \ ln (tu) = \ int _ {1} ^ {tu} {\ frac {1} {x}} \, dx \ {\ stackrel {(1)} {=}} \ int _ {1 } ^ {t} {\ frac {1} {x}} \, dx + \ int _ {t} ^ {tu} {\ frac {1} {x}} \, dx \ {\ stackrel {(2)} {=}} \ ln (t) + \ int _ {1} ^ {u} {\ frac {1} {w}} \, dw = \ ln (t) + \ ln (u).}$

Egalitatea (1) împarte integralul în două părți, în timp ce egalitatea (2) este o schimbare a variabilei ( w = x / t ). În ilustrația de mai jos, împărțirea corespunde împărțirii zonei în părțile galbene și albastre. Redimensionarea verticală a zonei albastre din stânga cu factorul  t și micșorarea acesteia cu același factor pe orizontală nu modifică dimensiunea acesteia. Deplasând-o corespunzător, zona se potrivește din nou cu graficul funcției f ( x ) = 1 / x . Prin urmare, zona albastră a mâinii stângi, care este integrala lui f ( x ) de la t la tu este aceeași cu integrala de la 1 la u . Acest lucru justifică egalitatea (2) cu o dovadă mai geometrică.

O dovadă vizuală a formulei produsului logaritmului natural

Formula de putere ln ( t ^r ) = r ln ( t ) poate fi derivată în mod similar:

${\ displaystyle \ ln (t ^ {r}) = \ int _ {1} ^ {t ^ {r}} {\ frac {1} {x}} dx = \ int _ {1} ^ {t} { \ frac {1} {w ^ {r}}} \ left (rw ^ {r-1} \, dw \ right) = r \ int _ {1} ^ {t} {\ frac {1} {w} } \, dw = r \ ln (t).}$

A doua egalitate utilizează o schimbare de variabile ( integrare prin substituție ), w = x ^{1 / r} .

Suma peste reciprocele numerelor naturale,

${\ displaystyle 1 + {\ frac {1} {2}} + {\ frac {1} {3}} + \ cdots + {\ frac {1} {n}} = \ sum _ {k = 1} ^ {n} {\ frac {1} {k}},}$

se numește seria armonică . Este strâns legat de logaritmul natural : pe măsură ce n tinde spre infinit , diferența,

${\ displaystyle \ sum _ {k = 1} ^ {n} {\ frac {1} {k}} - \ ln (n),}$

converge (adică devine arbitrar aproape) la un număr cunoscut sub numele constanta Euler-Mascheroni γ = 0.5772 ... . Această relație ajută la analiza performanței algoritmilor precum quicksort .

Transcendența logaritmului

Numerele reale care nu sunt algebrice se numesc transcendentale ; de exemplu, π și e sunt astfel de numere, dar nu este. Aproape toate numerele reale sunt transcendentale. Logaritmul este un exemplu de funcție transcendentală . Gelfond-Schneider teorema afirmă că logaritmi iau de obicei transcendentală, adică valori „dificile“. ${\ displaystyle {\ sqrt {2 - {\ sqrt {3}}}}}$

Calcul

Tastele logaritmice (LOG pentru baza 10 și LN pentru baza  e ) pe un calculator grafic TI-83 Plus

Logaritmii sunt ușor de calculat în unele cazuri, cum ar fi log ₁₀  (1000) = 3 . În general, logaritmii pot fi calculați utilizând serii de putere sau media aritmetică-geometrică sau pot fi extrase dintr-un tabel de logaritmi precalculat care oferă o precizie fixă. Metoda lui Newton , o metodă iterativă pentru a rezolva aproximativ ecuațiile, poate fi utilizată și pentru calcularea logaritmului, deoarece funcția sa inversă, funcția exponențială, poate fi calculată eficient. Folosind tabele de căutare, metodele de tip CORDIC pot fi folosite pentru a calcula logaritmi utilizând doar operațiile de adunare și schimbări de biți . Mai mult, algoritmul logaritmului binar calculează lb ( x ) recursiv , pe baza pătratelor repetate ale lui x , profitând de relația

${\ displaystyle \ log _ {2} \ left (x ^ {2} \ right) = 2 \ log _ {2} | x |.}$

Serie de puteri

Seria Taylor

Seria lui Taylor a ln ( z ) centrată la z = 1 . Animația arată primele 10 aproximări, împreună cu a 99-a și a 100-a. Aproximările nu converg dincolo de o distanță de 1 de centru.

Pentru orice număr real z care îndeplinește 0 < z ≤ 2 , se aplică următoarea formulă:

${\ displaystyle {\ begin {align} \ ln (z) & = {\ frac {(z-1) ^ {1}} {1}} - {\ frac {(z-1) ^ {2}} { 2}} + {\ frac {(z-1) ^ {3}} {3}} - {\ frac {(z-1) ^ {4}} {4}} + \ cdots \\ & = \ sum _ {k = 1} ^ {\ infty} (- 1) ^ {k + 1} {\ frac {(z-1) ^ {k}} {k}} \ end {align}}}$

Aceasta este o prescurtare pentru a spune că ln ( z ) poate fi aproximat la o valoare tot mai precisă prin următoarele expresii:

${\ displaystyle {\ begin {array} {lllll} (z-1) && \\ (z-1) & - & {\ frac {(z-1) ^ {2}} {2}} & \\ ( z-1) & - & {\ frac {(z-1) ^ {2}} {2}} & + & {\ frac {(z-1) ^ {3}} {3}} \\\ vdots & \ end {array}}}$

De exemplu, cu z = 1,5 a treia aproximare produce 0,4167, care este cu aproximativ 0,011 mai mare decât ln (1,5) = 0,405465 . Această serie aproximează ln ( z ) cu precizie arbitrară, cu condiția ca numărul sumandurilor să fie suficient de mare. În calculul elementar, ln ( z ) este, prin urmare, limita acestei serii. Este seria Taylor a logaritmului natural la z = 1 . Seria Taylor a ln ( z ) oferă o aproximare deosebit de utilă la ln (1 + z ) atunci când z este mic, | z | <1 , de atunci

${\ displaystyle \ ln (1 + z) = z - {\ frac {z ^ {2}} {2}} + {\ frac {z ^ {3}} {3}} \ cdots \ approx z.}$

De exemplu, cu z = 0,1 , aproximarea de prim ordin dă ln (1,1) ≈ 0,1 , ceea ce este mai mic de 5% din valoarea corectă 0,0953.

Serii mai eficiente

O altă serie se bazează pe funcția tangentă hiperbolică a zonei :

${\ displaystyle \ ln (z) = 2 \ cdot \ operatorname {artanh} \, {\ frac {z-1} {z + 1}} = 2 \ left ({\ frac {z-1} {z + 1 }} + {\ frac {1} {3}} {\ left ({\ frac {z-1} {z + 1}} \ right)} ^ {3} + {\ frac {1} {5}} {\ left ({\ frac {z-1} {z + 1}} \ right)} ^ {5} + \ cdots \ right),}$

pentru orice număr real z > 0 . Folosind notația sigma , aceasta este, de asemenea, scrisă ca

${\ displaystyle \ ln (z) = 2 \ sum _ {k = 0} ^ {\ infty} {\ frac {1} {2k + 1}} \ left ({\ frac {z-1} {z + 1 }} \ dreapta) ^ {2k + 1}.}$

Această serie poate fi derivată din seria Taylor de mai sus. Converge mai repede decât seria Taylor, mai ales dacă z este aproape de 1. De exemplu, pentru z = 1.5 , primii trei termeni din a doua serie aproximează ln (1.5) cu o eroare de aproximativ3 × 10 ⁻⁶ . Convergența rapidă pentru z apropiată de 1 poate fi profitată în felul următor: având o aproximare de precizie scăzută y ≈ ln ( z ) și

${\ displaystyle A = {\ frac {z} {\ exp (y)}},}$

logaritmul lui z este:

${\ displaystyle \ ln (z) = y + \ ln (A).}$

Cu cât este mai bună aproximarea inițială y , cu atât A este mai aproape de 1, deci logaritmul său poate fi calculat eficient. A poate fi calculat folosind seria exponențială , care converge rapid cu condiția ca y să nu fie prea mare. Calculul logaritmului z mai mare poate fi redus la valori mai mici ale z prin scrierea z = a · 10 ^b , astfel încât ln ( z ) = ln ( a ) + b · ln (10) .

O metodă strâns legată poate fi utilizată pentru a calcula logaritmul numerelor întregi. Introducând seria de mai sus, rezultă că: ${\ displaystyle \ textstyle z = {\ frac {n + 1} {n}}}$

${\ displaystyle \ ln (n + 1) = \ ln (n) +2 \ sum _ {k = 0} ^ {\ infty} {\ frac {1} {2k + 1}} \ left ({\ frac { 1} {2n + 1}} \ dreapta) ^ {2k + 1}.}$

Dacă se cunoaște logaritmul unui număr întreg  n , atunci această serie produce o serie convergentă rapidă pentru log ( n +1) , cu o rată de convergență de . ${\ textstyle \ left ({\ frac {1} {2n + 1}} \ right) ^ {2}}$

Aproximare medie aritmetică – geometrică

Media aritmetică-geometrică oferă aproximări de mare precizie ale logaritmului natural . Sasaki și Kanada au arătat în 1982 că este deosebit de rapid pentru precizii între 400 și 1000 zecimale, în timp ce metodele din seria Taylor erau de obicei mai rapide atunci când era nevoie de mai puțină precizie. În lucrarea lor ln ( x ) este aproximat la o precizie de 2 ^{- p} (sau p  biți preciși) prin următoarea formulă (datorită lui Carl Friedrich Gauss ):

${\ displaystyle \ ln (x) \ approx {\ frac {\ pi} {2 \, \ mathrm {M} \! \ left (1,2 ^ {2-m} / x \ right)}} - m \ ln (2).}$

Aici M ( x , y ) denotă media aritmetică-geometrică a lui x și y . Se obține calculând în mod repetat media ( x + y ) / 2 ( media aritmetică ) și ( media geometrică ) a lui x și y apoi lăsați aceste două numere să devină următoarele x și y . Cele două numere converg rapid către o limită comună care este valoarea lui M ( x , y ) . m este ales astfel încât ${\ textstyle {\ sqrt {xy}}}$

${\ displaystyle x \, 2 ^ {m}> 2 ^ {p / 2}. \,}$

pentru a asigura precizia necesară. Un m mai mare face ca calculul M ( x , y ) să facă mai mulți pași ( x inițial și y sunt mai îndepărtați, deci este nevoie de mai mulți pași pentru a converge), dar oferă mai multă precizie. Constantele π și ln (2) pot fi calculate cu serii care converg rapid.

Algoritmul lui Feynman

În timp ce lucra la Laboratorul Național Los Alamos la Proiectul Manhattan , Richard Feynman a dezvoltat un algoritm de procesare de biți care este similar cu divizarea lungă și a fost folosit ulterior în mașina de conectare . Algoritmul folosește faptul că fiecare număr real 1 < x <2 este reprezentabil ca produs al unor factori diferiți de forma 1 + 2 ^{- k} . Algoritmul construiește secvențial acel produs  P : dacă P · (1 + 2 ^{- k} ) < x , atunci se schimbă P în P · (1 + 2 ^{- k} ) . Apoi crește cu unul indiferent. Algoritmul se oprește când k este suficient de mare pentru a da acuratețea dorită. Deoarece log ( x ) este suma termenilor formularului log (1 + 2 ^{- k} ) corespunzător acelor k pentru care factorul 1 + 2 ^{- k a} fost inclus în produsul  P , log ( x ) poate fi calculat prin adăugare simplă, folosind un tabel de jurnal (1 + 2 ^{- k} ) pentru toate k . Orice bază poate fi utilizată pentru tabelul logaritmului. ${\ displaystyle k}$

Aplicații

Un nautilus care afișează o spirală logaritmică

Logaritmii au multe aplicații în interiorul și în afara matematicii. Unele dintre aceste apariții sunt legate de noțiunea de invarianță a scării . De exemplu, fiecare cameră a cochiliei unui nautilus este o copie aproximativă a celei următoare, scalată cu un factor constant. Aceasta dă naștere unei spirale logaritmice . Legea lui Benford privind distribuția cifrelor anterioare poate fi explicată și prin invarianța scării. Logaritmii sunt, de asemenea, legați de similitudinea de sine . De exemplu, logaritmii apar în analiza algoritmilor care rezolvă o problemă împărțind-o în două probleme similare mai mici și reparând soluțiile lor. Dimensiunile formelor geometrice auto-similare, adică formele ale căror părți seamănă cu imaginea de ansamblu se bazează, de asemenea, pe logaritmi. Scalele logaritmice sunt utile pentru cuantificarea schimbării relative a unei valori spre deosebire de diferența sa absolută. Mai mult, deoarece funcția logaritmică log ( x ) crește foarte încet pentru x mare , scările logaritmice sunt utilizate pentru a comprima date științifice la scară largă. Logaritmi , de asemenea , apar în numeroase formule științifice, cum ar fi ecuația Tsiolkovsky rachete , ecuația Fenske sau ecuația Nernst .

Scara logaritmică

O diagramă logaritmică care descrie valoarea unui Goldmark în Papiermarks în timpul hiperinflației germane din anii 1920

Mărimile științifice sunt adesea exprimate ca logaritmi ai altor mărimi, utilizând o scară logaritmică . De exemplu, decibelul este o unitate de măsură asociată cu mărimi la scară logaritmică . Se bazează pe logaritmul comun al raporturilor - de 10 ori logaritmul comun al unui raport de putere sau de 20 de ori logaritmul comun al unui raport de tensiune . Este folosit pentru a cuantifica pierderea nivelurilor de tensiune în transmiterea semnalelor electrice, pentru a descrie nivelurile de putere ale sunetelor în acustică și absorbția luminii în câmpurile de spectrometrie și optică . Raportul semnal-zgomot care descrie cantitatea de zgomot nedorit în raport cu un semnal (semnificativ) este, de asemenea, măsurat în decibeli. Într-un mod similar, raportul de vârf semnal-zgomot este utilizat în mod obișnuit pentru a evalua calitatea metodelor de compresie a sunetului și a imaginii folosind logaritmul.

Puterea unui cutremur este măsurată luând logaritmul comun al energiei emise la cutremur. Aceasta este utilizată în scara magnitudinii momentului sau în scara magnitudinii Richter . De exemplu, un cutremur de 5.0 eliberează de 32 de ori (10 ^1.5 ) și un 6.0 eliberează de 1000 de ori (10 ³ ) energia unui 4.0. Magnitudinea aparentă măsoară luminozitatea stelelor logaritmic. În chimie , negativul logaritmului zecimal, cologaritmul zecimal, este indicat de litera p. De exemplu, pH - ul este cologarithm zecimal al activității de hidroniu ioni (forma hidrogen ionii H⁺
luați apă). Activitatea ionilor de hidroniu în apa neutră este de 10 ⁻⁷  mol·L ⁻¹ , deci un pH de 7. Oțetul are de obicei un pH de aproximativ 3. Diferența de 4 corespunde unui raport de 10 ⁴ din activitate, adică , activitatea ionului de hidroniu al oțetului este de aproximativ 10 ⁻³ mol·L ⁻¹ .

Graficele semilogale (log-liniare) utilizează conceptul de scară logaritmică pentru vizualizare: o axă, de obicei cea verticală, este scalată logaritmic. De exemplu, graficul din dreapta comprimă creșterea abruptă de la 1 milion la 1 trilion în același spațiu (pe axa verticală) ca creșterea de la 1 la 1 milion. În astfel de grafice, funcțiile exponențiale ale formei f ( x ) = a · b ^x apar ca linii drepte cu panta egală cu logaritmul lui b . Graficele log-log scalează ambele axe logaritmic, ceea ce face ca funcțiile formei f ( x ) = a · x ^k să fie reprezentate ca linii drepte cu panta egală cu exponentul  k . Acest lucru se aplică în vizualizarea și analizarea legilor puterii .

Psihologie

Logaritmii apar în mai multe legi care descriu percepția umană : legea lui Hick propune o relație logaritmică între timpul pe care îl iau indivizii pentru a alege o alternativă și numărul de alegeri pe care le au. Legea lui Fitts prezice că timpul necesar pentru mutarea rapidă într-o zonă țintă este o funcție logaritmică a distanței și a dimensiunii țintei. În psihofizică , legea Weber-Fechner propune o relație logaritmică între stimul și senzație, cum ar fi greutatea reală față de greutatea percepută a unui obiect pe care îl poartă o persoană. (Această „lege” este totuși mai puțin realistă decât modelele mai recente, cum ar fi legea puterii lui Stevens .)

Studiile psihologice au constatat că indivizii cu puțină educație matematică tind să estimeze cantitățile logaritmic, adică poziționează un număr pe o linie nemarcată conform logaritmului său, astfel încât 10 este poziționat la fel de aproape 100, 100 fiind la 1000. Creșterea educației schimbă acest lucru la o estimare liniară (poziționând de 1000 de ori mai departe) în anumite circumstanțe, în timp ce se utilizează logaritmi atunci când numerele care urmează a fi reprezentate sunt dificil de trasat liniar.

Teoria probabilității și statisticile

Trei funcții de densitate de probabilitate (PDF) ale variabilelor aleatorii cu distribuții log-normale. Parametrul de localizare  μ , care este zero pentru toate cele trei PDF-uri afișate, este media logaritmului variabilei aleatoare, nu media variabilei în sine.

Distribuția primelor cifre (în%, bare roșii) în populația din cele 237 de țări ale lumii. Punctele negre indică distribuția prezisă de legea lui Benford.

Logaritmii apar în teoria probabilității : legea numărului mare dictează că, pentru o monedă corectă , pe măsură ce numărul de aruncări de monede crește la infinit, proporția observată de capete se apropie de jumătate . Fluctuațiile acestei proporții aproximativ jumătate sunt descrise de legea logaritmului iterat .

Logaritmii apar și în distribuțiile log-normale . Când logaritmul unei variabile aleatorii are o distribuție normală , se spune că variabila are o distribuție log-normală. Distribuțiile log-normale sunt întâlnite în multe domenii, oriunde se formează o variabilă ca produs al multor variabile aleatorii pozitive independente, de exemplu în studiul turbulenței.

Logaritmii sunt utilizați pentru estimarea maximă a probabilității modelelor statistice parametrice . Pentru un astfel de model, funcția de probabilitate depinde de cel puțin un parametru care trebuie estimat. Un maxim al funcției de probabilitate apare la același parametru-valoare ca un maxim al logaritmului probabilității („ log probabilitatea ”), deoarece logaritmul este o funcție în creștere. Probabilitatea jurnalului este mai ușor de maximizat, în special pentru probabilitățile multiplicate pentru variabilele aleatoare independente .

Legea lui Benford descrie apariția cifrelor în multe seturi de date , cum ar fi înălțimile clădirilor. Conform legii lui Benford, probabilitatea ca prima cifră zecimală a unui articol din eșantionul de date să fie d (de la 1 la 9) este egală cu log ₁₀  ( d + 1) - log ₁₀  ( d ) , indiferent de unitatea de măsură. Astfel, aproximativ 30% din date se poate aștepta să aibă 1 ca primă cifră, 18% încep cu 2 etc. Auditorii examinează abaterile de la legea lui Benford pentru a detecta contabilitatea frauduloasă.

Complexitatea computațională

Analiza algoritmilor este o ramură a științei de calculator , care studiază performanța de algoritmi (programe pentru calculator rezolva o anumită problemă). Logaritmii sunt valoroși pentru descrierea algoritmilor care împart o problemă în altele mai mici și se alătură soluțiilor subproblemelor.

De exemplu, pentru a găsi un număr într-o listă sortată, algoritmul de căutare binară verifică intrarea din mijloc și continuă cu jumătatea înainte sau după intrarea din mijloc, dacă numărul nu este încă găsit. Acest algoritm necesită, în medie, comparații log ₂  ( N ) , unde N este lungimea listei. În mod similar, algoritmul de sortare a fuzionării sortează o listă nesortată împărțind lista în jumătăți și sortându-le mai întâi înainte de a fuziona rezultatele. Algoritmii de sortare Merge necesită de obicei un timp aproximativ proporțional cu N · log ( N ) . Baza logaritmului nu este specificată aici, deoarece rezultatul se modifică doar cu un factor constant atunci când este utilizată o altă bază. Un factor constant este de obicei ignorat în analiza algoritmilor în cadrul modelului standard de cost uniform .

Se spune că o funcție  f ( x ) crește logaritmic dacă f ( x ) este (exact sau aproximativ) proporțional cu logaritmul lui x . (Cu toate acestea, descrierile biologice ale creșterii organismului folosesc acest termen pentru o funcție exponențială.) De exemplu, orice număr natural  N poate fi reprezentat în formă binară în cel mult log ₂  N + 1  biți . Cu alte cuvinte, cantitatea de memorie necesară pentru a stoca N crește logaritmic cu N .

Entropie și haos

Biliard pe o masă de biliard ovală . Două particule, pornind de la centru cu un unghi diferit de un grad, iau căi care diverg haotic din cauza reflexiilor la limită.

Entropia este, în linii mari, o măsură a tulburării unui sistem. În termodinamica statistică , entropia  S a unui sistem fizic este definită ca

${\ displaystyle S = -k \ sum _ {i} p_ {i} \ ln (p_ {i}). \,}$

Suma este peste toate stările posibile  i ale sistemului în cauză, cum ar fi pozițiile particulelor de gaz într-un container. Mai mult, p _i este probabilitatea ca starea  i să fie atinsă și k este constanta Boltzmann . În mod similar, entropia în teoria informației măsoară cantitatea de informații. Dacă un destinatar al mesajului se poate aștepta la oricare dintre N mesaje posibile cu probabilitate egală, atunci cantitatea de informații transmise de oricare astfel de mesaj este cuantificată ca log ₂  N biți.

Exponenții Lyapunov folosesc logaritmi pentru a măsura gradul de haotică al unui sistem dinamic . De exemplu, pentru o particulă care se mișcă pe o masă de biliard ovală, chiar și mici modificări ale condițiilor inițiale duc la căi foarte diferite ale particulei. Astfel de sisteme sunt haotice într-un mod determinist , deoarece erorile mici de măsurare ale stării inițiale conduc în mod previzibil la stări finale în mare măsură diferite. Cel puțin un exponent Lyapunov al unui sistem haotic determinist este pozitiv.

Fractale

Triunghiul Sierpinski (în dreapta) este construit prin înlocuirea repetată a triunghiurilor echilaterale cu trei mai mici.

Logaritmi apar în definiții ale dimensiunii de fractali . Fractalele sunt obiecte geometrice care se aseamănă cu sine : părțile mici reproduc, cel puțin aproximativ, întreaga structură globală. Sierpinski triunghi (foto) poate fi acoperit de trei exemplare în sine, fiecare având părți jumătate din lungimea inițială. Acest lucru face ca dimensiunea Hausdorff a acestei structuri să fie ln (3) / ln (2) ≈ 1,58 . O altă noțiune de dimensiune bazată pe logaritm este obținută prin numărarea numărului de casete necesare pentru acoperirea fractalului în cauză.

Muzică

Patru octave diferite prezentate pe o scară liniară, apoi afișate pe o scară logaritmică (pe măsură ce urechea le aude).

Logaritmii sunt legați de tonuri și intervale muzicale . În egală temperament , raportul de frecvență depinde numai de intervalul dintre două tonuri, nu pe frecvența specifică, sau teren , a tonurilor individuale. De exemplu, nota  A are o frecvență de 440  Hz, iar bemol are o frecvență de 466 Hz. Intervalul dintre A și B bemol este un semiton , la fel ca și cel dintre B bemol și B (frecvență 493 Hz). În consecință, raporturile de frecvență sunt de acord:

${\ displaystyle {\ frac {466} {440}} \ approx {\ frac {493} {466}} \ approx 1.059 \ approx {\ sqrt [{12}] {2}}.}$

Prin urmare, logaritmii pot fi folosiți pentru a descrie intervalele: un interval este măsurat în semitonuri luând logaritmul de bază - 2 ^1/12 al raportului de frecvență , în timp ce logaritmul de bază - 2 ^1/1200 al raportului de frecvență exprimă intervalul în cenți , sutimi de semiton. Acesta din urmă este utilizat pentru o codificare mai fină, deoarece este necesar pentru temperamente care nu sunt egale.

Interval (cele două tonuri sunt redate în același timp)	Redare 1/12 ton ( ajutor · informații )	Piesa de semiton	Doar a treia piesă majoră	A treia piesă majoră	Piesa de triton	Joc de octavă
Raportul de frecvență r	${\ displaystyle 2 ^ {\ frac {1} {72}} \ approx 1.0097}$	${\ displaystyle 2 ^ {\ frac {1} {12}} \ approx 1.0595}$	${\ displaystyle {\ tfrac {5} {4}} = 1,25}$	${\ displaystyle {\ begin {align} 2 ^ {\ frac {4} {12}} & = {\ sqrt [{3}] {2}} \\ & \ approx 1.2599 \ end {align}}}$	${\ displaystyle {\ begin {align} 2 ^ {\ frac {6} {12}} & = {\ sqrt {2}} \\ & \ approx 1.4142 \ end {align}}}$	${\ displaystyle 2 ^ {\ frac {12} {12}} = 2}$
Numărul corespunzător de semitonuri ${\ displaystyle \ log _ {\ sqrt [{12}] {2}} (r) = 12 \ log _ {2} (r)}$	${\ displaystyle {\ tfrac {1} {6}}}$	${\ displaystyle 1}$	${\ displaystyle \ approx 3.8631}$	${\ displaystyle 4}$	${\ displaystyle 6}$	${\ displaystyle 12}$
Numărul corespunzător de cenți ${\ displaystyle \ log _ {\ sqrt [{1200}] {2}} (r) = 1200 \ log _ {2} (r)}$	${\ displaystyle 16 {\ tfrac {2} {3}}}$	${\ displaystyle 100}$	${\ displaystyle \ approx 386.31}$	${\ displaystyle 400}$	${\ displaystyle 600}$	${\ displaystyle 1200}$

Teoria numerelor

Logaritmii naturali sunt strâns legați de numărarea numerelor prime (2, 3, 5, 7, 11, ...), un subiect important în teoria numerelor . Pentru orice număr întreg  x , cantitatea numerelor prime mai mici sau egale cu x se notează π ( x ) . Numărul prim teorema afirmă că π ( x ) este dată de aproximativ

${\ displaystyle {\ frac {x} {\ ln (x)}},}$

în sensul că raportul dintre π ( x ) și acea fracție se apropie de 1 când x tinde spre infinit. În consecință, probabilitatea ca un număr ales aleatoriu între 1 și x să fie primă este invers proporțională cu numărul de cifre zecimale ale lui x . O estimare mult mai bună a π ( x ) este dată de funcția integrală logaritmică decalată Li ( x ) , definită de

${\ displaystyle \ mathrm {Li} (x) = \ int _ {2} ^ {x} {\ frac {1} {\ ln (t)}} \, dt.}$

Ipoteza Riemann , una dintre cele mai vechi matematice deschise conjecturilor , se poate afirma , în ceea ce privește compararea π ( x ) și Li ( x ) . Teorema Erdős-Kac care descrie numărul de distincte factori prime implică și logaritmul natural .

Logaritmul n factorial , n ! = 1 · 2 · ... · n , este dat de

${\ displaystyle \ ln (n!) = \ ln (1) + \ ln (2) + \ cdots + \ ln (n).}$

Aceasta poate fi utilizată pentru a obține formula lui Stirling , o aproximare de n ! pentru n mare .

Generalizări

Logaritm complex

Forma polară a z = x + iy . Atât φ cât și φ ' sunt argumente ale lui z .

Toate numerele complexe a care rezolvă ecuația

${\ displaystyle e ^ {a} = z}$

sunt numite logaritmi complexi ai lui z , când z este (considerat ca) un număr complex. Un număr complex este de obicei reprezentat ca z = x + iy , unde x și y sunt numere reale și i este o unitate imaginară , al cărei pătrat este -1. Un astfel de număr poate fi vizualizat de un punct din planul complex , așa cum se arată în dreapta. Forma polară codifică un număr complex diferit de  z prin valoarea sa absolută , adică distanța (pozitivă, reală)  r la origine și un unghi între axa reală ( x ) Re și linia care trece prin ambele origini și z . Acest unghi se numește argumentul lui z .  

Valoarea absolută r a z este dată de

${\ displaystyle \ textstyle r = {\ sqrt {x ^ {2} + y ^ {2}}}.}$

Folosind interpretarea geometrică a sinusului și cosinusului și periodicitatea lor în 2 π , orice număr complex  z poate fi notat ca

${\ displaystyle z = x + iy = r (\ cos \ varphi + i \ sin \ varphi) = r (\ cos (\ varphi + 2k \ pi) + i \ sin (\ varphi + 2k \ pi)),}$

pentru orice număr întreg  k . Evident, argumentul lui z nu este specificat în mod unic: atât φ cât și φ ' = φ + 2 k π sunt argumente valide ale z pentru toate numerele întregi  k , deoarece adăugarea a 2 k π  radiani sau k ⋅360 ° la φ corespunde „înfășurării” în jurul originea în sens invers acelor de ceasornic cu k  se întoarce . Numărul complex rezultat este întotdeauna z , așa cum se ilustrează în dreapta pentru k = 1 . Se poate selecta exact unul dintre argumentele posibile ale z ca așa-numitul argument principal , denumit Arg ( z ) , cu majusculă  A , cerând ca φ să aparțină unui singur viraj selectat convenabil, de exemplu - π < φ ≤ π sau 0 ≤ φ <2 π . Aceste regiuni, unde argumentul lui z este determinat în mod unic, se numesc ramuri ale funcției de argument.

Ramura principală (- π , π ) a logaritmului complex, Log ( z ) . Punctul negru la z = 1 corespunde valorii absolute zero și culorile mai strălucitoare, mai saturate , se referă la valori absolute mai mari. Nuanța culorii codifică argumentul Log ( z ) .

Formula lui Euler conectează funcțiile trigonometrice sinus și cosinus la exponențialul complex :

${\ displaystyle e ^ {i \ varphi} = \ cos \ varphi + i \ sin \ varphi.}$

Folosind această formulă și din nou periodicitatea, se păstrează următoarele identități:

${\ displaystyle {\ begin {array} {lll} z & = & r \ left (\ cos \ varphi + i \ sin \ varphi \ right) \\ & = & r \ left (\ cos (\ varphi + 2k \ pi) + i \ sin (\ varphi + 2k \ pi) \ right) \\ & = & re ^ {i (\ varphi + 2k \ pi)} \\ & = & e ^ {\ ln (r)} e ^ {i (\ varphi + 2k \ pi)} \\ & = & e ^ {\ ln (r) + i (\ varphi + 2k \ pi)} = e ^ {a_ {k}}, \ end {array}}}$

unde ln ( r ) este logaritmul natural real unic, a _k denotă logaritmii complecși ai lui z și k este un număr întreg arbitrar. Prin urmare, logaritmii complexi ai lui z , care sunt toate acele valori complexe a _k pentru care puterea a _k -  a lui e este egală cu z , sunt infinit de multe valori

${\ displaystyle a_ {k} = \ ln (r) + i (\ varphi + 2k \ pi), \ quad}$pentru numere întregi arbitrare  k .

Luând k astfel încât φ + 2 k π să fie în intervalul definit pentru argumentele principale, atunci a _k se numește valoarea principală a logaritmului, notat Log ( z ) , din nou cu un  L mare . Argumentul principal al oricărui număr real pozitiv  x este 0; prin urmare Log ( x ) este un număr real și este egal cu logaritmul real (natural). Cu toate acestea, formulele de mai sus pentru logaritmii produselor și puterilor nu se generalizează la valoarea principală a logaritmului complex.

Ilustrația din dreapta ilustrează Log ( z ) , limitând argumentele lui z la intervalul (−π, π] . Astfel, ramura corespunzătoare a logaritmului complex are discontinuități de-a lungul  axei x reale negative , care poate fi văzută în saltul în nuanță de acolo. Această discontinuitate apare din săritura către cealaltă limită din aceeași ramură, atunci când traversează o limită, adică nu se schimbă la valoarea k corespunzătoare a ramurii vecine continuu. Un astfel de locus se numește tăietură de ramură . Eliminarea restricțiilor de interval asupra argumentului face ca relațiile să fie „argumentul lui z ” și, în consecință, „logaritmul lui z ”, funcții cu mai multe valori .

Inversele altor funcții exponențiale

Exponențierea are loc în multe domenii ale matematicii și funcția sa inversă este adesea denumită logaritm. De exemplu, logaritmul unei matrice este funcția inversă (multivalentă) a exponențialei matricei . Un alt exemplu este logaritmul p -adic , funcția inversă a exponențialei p -adic . Ambele sunt definite prin intermediul seriei Taylor analog cazului real. În contextul geometriei diferențiale , harta exponențială mapează spațiul tangent la un punct al unei varietăți la un vecinătate al acelui punct. Inversul său se mai numește hartă logaritmică (sau log).

În contextul grupurilor finite, exponențierea este dată de înmulțirea repetată a unui element de grup  b cu el însuși. Logaritmul discret este întreg  n rezolvarea ecuației

${\ displaystyle b ^ {n} = x,}$

unde x este un element al grupului. Realizarea exponențierii se poate face eficient, dar se crede că logaritmul discret este foarte greu de calculat în unele grupuri. Această asimetrie are aplicații importante în criptografia cu chei publice , cum ar fi, de exemplu, în schimbul de chei Diffie – Hellman , o rutină care permite schimburi sigure de chei criptografice pe canale de informații nesecurizate. Logaritmul lui Zech este legat de logaritmul discret din grupul multiplicativ al elementelor nenule ale unui câmp finit .

Alte funcții inverse asemănătoare logaritmului includ logaritmul dublu  ln (ln ( x )) , super- sau hiper-4-logaritmul (a cărui ușoară variație se numește logaritm iterat în informatică), funcția Lambert W și logit . Ele sunt funcțiile inverse ale funcției exponențiale duble , tetrare , a lui f ( w ) = we ^w și , respectiv, a funcției logistice .

Concepte conexe

Din perspectiva teoriei grupurilor , logul identității ( cd ) = log ( c ) + log ( d ) exprimă un izomorfism de grup între realii pozitivi sub multiplicare și realii sub adunare. Funcțiile logaritmice sunt singurele izomorfisme continue dintre aceste grupuri. Prin intermediul acestui izomorfism, măsura Haar ( măsura Lebesgue )  dx pe reali corespunde măsurii Haar  dx / x pe realii pozitivi. Realii non-negativi nu numai că au o înmulțire, dar au și adunare și formează o semire , numită semiremediabilă de probabilitate ; acesta este de fapt un semicamp . Logaritmul ia apoi înmulțirea la adunare (înmulțirea jurnalului) și ia adaosul la adunarea jurnalului ( LogSumExp ), oferind un izomorfism al semiroturilor între semirelevabilitatea probabilității și semirotarea jurnalului .

Formele unice logaritmice  df / f apar în analiza complexă și geometria algebrică ca forme diferențiale cu poli logaritmici .

Polylogarithm este funcția definită de

${\ displaystyle \ operatorname {Li} _ {s} (z) = \ sum _ {k = 1} ^ {\ infty} {z ^ {k} \ over k ^ {s}}.}$

Este legat de logaritmul natural prin Li ₁  ( z ) = −ln (1 - z ) . Mai mult, Li _s  (1) este egală cu funcția zeta Riemann ζ ( s ) .

Vezi si

• Cologaritm
• Exponent zecimal (dex)
• Functie exponentiala
• Indexul articolelor logaritmice
• Notatie logaritmica

Note

Referințe

linkuri externe

• Medii legate de Logaritm la Wikimedia Commons
• Definiția dicționarului de logaritm la Wikționar
• Weisstein, Eric W. , „Logaritm” , MathWorld
• Academia Khan: Logaritmi, microcursuri online gratuite
• „Funcția logaritmică” , Enciclopedia Matematicii , EMS Press , 2001 [1994]
• Colin Byfleet, Video educațional despre logaritmi , accesat la 12 octombrie 2010
• Edward Wright, Traducerea lucrării lui Napier despre logaritmi , arhivată din original la 3 decembrie 2002 , recuperată la 12 octombrie 2010CS1 maint: URL inadecvat ( link )
• Glaisher, James Whitbread Lee (1911), „Logaritm”  , în Chisholm, Hugh (ed.), Encyclopædia Britannica , 16 (ediția a XI-a), Cambridge University Press, pp. 868-77