Cutie Edgeworth - Edgeworth box
În economie , o cutie Edgeworth, denumită uneori o cutie Edgeworth-Bowley, este o reprezentare grafică a unei piețe cu doar două mărfuri, X și Y și doi consumatori. Dimensiunile cutiei sunt cantitățile totale Ω x și Ω y ale celor două bunuri.
Consumatorii să fie Octavio și Abby. Colțul din dreapta sus al casetei reprezintă alocarea în care Octavio deține toate bunurile, în timp ce partea din stânga jos corespunde proprietății complete a lui Abby. Punctele din casetă reprezintă modalități de repartizare a bunurilor între cei doi consumatori.
Comportamentul pieței va fi determinat de curbele de indiferență ale consumatorilor . Curbele albastre din diagramă reprezintă curbe de indiferență pentru Octavio și sunt prezentate ca convexe din punctul său de vedere (adică văzut din stânga jos). Curbele portocalii se aplică lui Abby și sunt convexe așa cum se vede din dreapta sus. Deplasarea în sus și spre dreapta mărește alocarea lui Octavio și îl pune pe o curbă de indiferență mai dorită în timp ce îl plasează pe Abby pe una mai puțin dorită.
Curbele de indiferență convexe sunt considerate a fi cazul obișnuit. Ele corespund randamentelor diminuate pentru fiecare bun în raport cu celălalt.
Schimbul pe piață începe de la o alocare inițială cunoscută sub numele de dotare .
Principala utilizare a casetei Edgeworth este de a introduce subiecte în teoria generală a echilibrului într-o formă în care proprietățile pot fi vizualizate grafic. De asemenea, poate arăta dificultatea de a trece la un rezultat eficient în prezența monopolului bilateral . În acest din urmă caz, servește ca un precursor al problemei de negociere a teoriei jocurilor care permite o soluție numerică unică.
Istorie
Dezvoltarea casetei Edgeworth
Cutia Edgeworth poartă numele lui Francis Ysidro Edgeworth , care a prezentat-o în cartea sa Mathematical Psychics: An Essay on the Application of Mathematics to the Moral Sciences , 1881. Imaginea originală pe două axe a lui Edgeworth a fost dezvoltată în diagrama de cutie acum familiară de Pareto în Manualul său de economie politică din 1906 și a fost popularizat într-o expoziție ulterioară de către Bowley . Versiunea modernă a diagramei este denumită în mod obișnuit caseta Edgeworth – Bowley .
Teoria matematică a echilibrului economic
Cadrul conceptual al echilibrului într-o economie de piață a fost dezvoltat de Léon Walras și extins în continuare de Vilfredo Pareto . A fost examinat cu mare atenție la generalitate și rigoare de către economiștii matematici ai secolului al XX-lea, inclusiv Abraham Wald , Paul Samuelson , Kenneth Arrow și Gérard Debreu . Aceasta a făcut parte dintr-o mișcare mai largă în care Wald a căutat, de asemenea, să aducă o mai mare rigoare teoriei deciziilor, iar mulți matematicieni s-au concentrat pe minimizarea dependenței de axioma de alegere .
Teoria piețelor Walrasiene s-a străduit să găsească cele mai generale premise din care se poate obține o concluzie dată. Domeniile în care spațiile pot fi întărite sau slăbite includ:
- Dacă funcțiile sunt diferențiate;
- Dacă curbele de indiferență sunt primitive sau derivabile din funcțiile utilitare ; și
- Indiferent dacă curbele de indiferență sunt convexe.
Ipotezele sunt, de asemenea, făcute cu o natură mai tehnică, de exemplu, non-reversibilitate, saturație etc.
Căutarea rigorii nu este întotdeauna favorabilă inteligibilității. În acest articol, curbele de indiferență vor fi tratate ca primitive. La început le vom vedea ca fiind convexe și diferențiate și ne vom concentra asupra echilibrelor interioare, dar ulterior vom relaxa aceste ipoteze.
Echilibrul pieței
Deoarece există doar două mărfuri, prețul efectiv este cursul de schimb dintre ele. Scopul nostru este de a găsi prețul la care poate fi atins echilibrul pieței, care va fi un punct în care nu se doresc alte tranzacții, începând de la o dotare dată. Aceste cantități vor fi determinate de curbele de indiferență ale celor doi consumatori, așa cum se arată în figura 2.
Vom presupune că Octavio și Abby merg zilnic pe piață cu dotări (ω x , ω y ) și (Ω x - ω x , Ω y - ω y ) ale celor două mărfuri, corespunzătoare poziției ω din diagramă. Cei doi consumatori vor face schimburi între ei sub un comportament concurențial pe piață. Această presupunere necesită o anumită suspendare a necredinței, deoarece condițiile pentru o concurență perfectă - care includ un număr infinit de consumatori - nu sunt îndeplinite.
Dacă doi X schimbă un singur Y , atunci tranzacția lui Octavio și Abby îi va duce la un moment dat de-a lungul liniei gri solide, cunoscută sub numele de linie bugetară . (Pentru a fi mai precis, o linie bugetară poate fi definită ca o linie dreaptă prin punctul de dotare reprezentând alocații care pot fi obținute prin schimb la un anumit preț.) Liniile bugetare pentru câteva alte prețuri sunt, de asemenea, prezentate ca linii punctate și punctate în Fig. 2.
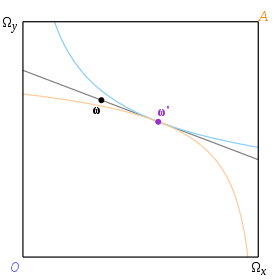
Echilibrul corespunzător unei înzestrări date ω este determinat de perechea de curbe de indiferență care au o tangentă comună astfel încât această tangentă să treacă prin ω . Vom folosi termenul „linie de preț” pentru a desemna o tangentă comună la două curbe de indiferență. Prin urmare, un echilibru corespunde unei linii bugetare care este și o linie de preț, iar prețul la equlibrium este gradientul liniei. În Fig. 3 ω este dotarea și ω ' este alocarea equlibrium.
Raționamentul din spatele acestui lucru este următorul.
În primul rând, orice punct din cutie trebuie să se afle exact pe una dintre curbele de indiferență a lui Abby și exact pe una dintre Octavio. Dacă curbele se încrucișează (așa cum se arată în Fig. 4), atunci acestea împart vecinătatea imediată în patru regiuni, dintre care una (arătată ca verde pal) este preferabilă pentru ambii consumatori; prin urmare, un punct în care curbele de indiferență se încrucișează nu pot fi un equlibrium, iar un echilibru trebuie să fie un punct de tangență.
În al doilea rând, singurul preț care poate fi păstrat pe piață la punctul de tangență este cel dat de gradientul tangentei, deoarece doar la acest preț, consumatorii vor fi dispuși să accepte schimburi limitativ de mici.
Și în al treilea rând (cel mai dificil punct) toate schimburile care duc consumatorii pe calea de la ω la echilibru trebuie să aibă loc la același preț. Dacă acest lucru este acceptat, atunci acel preț trebuie să fie cel operativ la punctul de tangență și rezultatul urmează.
Într-o economie cu două persoane nu există nicio garanție că toate schimburile vor avea loc la același preț. Dar scopul casetei Edgeworth nu este să ilustreze stabilirea prețurilor care poate avea loc atunci când nu există concurență, ci mai degrabă să ilustreze o economie competitivă într-un caz minim. Așa că ne putem imagina că, în loc de un singur Abby și un singur Octavio, avem un număr infinit de clone din fiecare, toate venind pe piață cu dotări identice în momente diferite și care își negociază treptat drumul spre echilibru. Un Octavio nou sosit poate schimba la prețul pieței cu un Abby care este aproape de echilibru și, atâta timp cât un Abby nou sosit schimbă cu un Octavio aproape mulțumit, numerele se vor echilibra. Pentru ca schimbul să lucreze într-o mare economie competitivă, același preț trebuie să domnească pentru toată lumea. Astfel, schimbul trebuie să mute alocarea de-a lungul liniei de preț așa cum am definit-o.
Sarcina de a găsi un echilibru competitiv se reduce în consecință la sarcina de a găsi un punct de tangență între două curbe de indiferență pentru care tangenta trece printr-un punct dat. Utilizarea curbelor ofertei (descrisă mai jos) oferă o procedură sistematică pentru a face acest lucru.
Set Pareto
Se spune că o alocare de bunuri „Pareto domină” alta dacă este preferabilă pentru un consumator și nu mai gravă pentru celălalt. Se spune că o alocare este „ Pareto optimă ” (sau „Pareto eficientă”) dacă nicio altă alocare Pareto nu o domină. Setul de alocări optime Pareto este cunoscut sub numele de set Pareto (sau „locus eficient”).
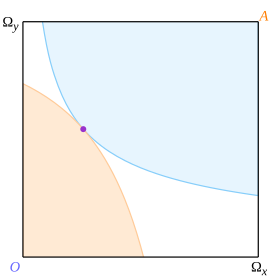
Luați în considerare o pereche de curbe tangențiale, una pentru fiecare consumator așa cum este ilustrat în Fig. 5, unde punctul de tangență este prezentat de punctul purpuriu. Apoi convexitatea garantează că curbele nu pot intercepta decât în punctul de tangență și căsuța este împărțită în consecință în 3 regiuni. Zona albastră pal este preferabilă punctului de tangență pentru Octavio, dar mai rău pentru Abby; zona portocaliu pal este de preferat pentru Abby, dar mai rău pentru Octavio; iar zona albă este mai rea pentru ambele. Considerații similare se aplică granițelor. Rezultă că punctul de tangență este Pareto optim.
Astfel mulțimea Pareto este locul punctelor de tangență ale curbelor. Aceasta este o linie care leagă originea lui Octavio (O) de Abby (A). Un exemplu este prezentat în Fig. 6, unde linia purpurie este setul Pareto corespunzător curbelor de indiferență pentru cei doi consumatori.
Vocabularul folosit pentru a descrie diferite obiecte care fac parte din caseta Edgeworth diferă. Întregul set Pareto este uneori numit curba contractuală , în timp ce Mas-Colell și colab. restrângeți definiția curbei contractului la acele puncte din setul Pareto care fac atât Abby, cât și Octavio cel puțin la fel de bine pe cât sunt la dotarea lor inițială. Alți autori care au o îndoială mai teoretică a jocului , cum ar fi Martin Osborne și Ariel Rubinstein , folosesc termenul de bază pentru secțiunea setului Pareto, care este cel puțin la fel de bun pentru fiecare consumator ca dotarea inițială.
Deoarece setul Pareto este setul de puncte în care curbele de indiferență ale consumatorilor sunt tangențiale, este și setul de puncte în care rata marginală de substituție a fiecărui consumator este egală cu cea a celeilalte persoane.
Prima teoremă fundamentală a economiei bunăstării
Am văzut că punctele de tangență ale curbelor de indiferență sunt optima Pareto, dar am văzut și anterior că echilibrele economice sunt acele puncte în care curbele de indiferență sunt tangențiale la o linie de preț comună. Rezultă că echilibrele sunt tocmai Pareto optima.
Acest argument se aplică cu o singură restricție chiar dacă curbele sunt nediferențiate sau dacă echilibrul se află la graniță. Condiția pentru echilibru este aceea că nu va mai avea loc niciun schimb, iar condiția ca să nu mai aibă loc un schimb este că nu există o direcție de mișcare care să beneficieze un consumator fără a-l afecta pe celălalt; iar acest lucru este echivalent cu definiția unui optim Pareto.
Restricția este că echilibrul implică faptul că nu se poate face nicio îmbunătățire locală - cu alte cuvinte, că punctul este „local” Pareto optim. Dar optimitatea Pareto este considerată astăzi globală prin definiție. Astfel, dacă natura curbelor de indiferență permite să apară optime non-globale (așa cum nu se poate întâmpla dacă sunt convexe), atunci este posibil ca echilibrele să nu fie Pareto optim.
Concurența perfectă nu este o condiție prealabilă pentru teoremă. Atâta timp cât consumatorii sunt liberi să facă schimb și vor continua să facă acest lucru până când nu este disponibil un schimb reciproc acceptabil, echilibrul va fi atins și va fi (cel puțin „local”) Pareto optim.
A doua teoremă fundamentală a economiei bunăstării
Acum luați în considerare o economie în care consumatorii au dotări ω așa cum se arată în Fig. 7. Lăsată în sine o piață liberă îi va duce la ω ' . Dar să presupunem că o altă poziție din casetă - să spunem α ' - este considerată preferabilă din punct de vedere social. Putem presupune că poziția dorită social este Pareto optimă.
S-ar putea să credem că liniile de prețuri (prezentate în linie în diagramă) corespund diferitelor distribuții ale venitului real și că ne deplasăm de-a lungul acestora ca realocare a resurselor în timp ce veniturile rămân fixe.
Apoi, pentru a repoziționa societatea în punctul dorit α ' , nu este necesar ca guvernul să redistribuie resursele în așa fel încât Octavio să dețină (α' x , α ' y ) și Abby să dețină complementul: este suficient să realocăm resursele pentru a duce economia în orice punct (să zicem α ) de pe linia de preț prin α ' și apoi să părăsim piața pentru a-și găsi propriul echilibru. Într-adevăr, atâta timp cât guvernul recunoaște o distribuție dorită a veniturilor, nu trebuie să aibă nicio idee despre alocarea optimă a resurselor.
Într-o declarație pentru o economie mai generală, teorema ar fi considerată ca spunând că α ' poate fi atins printr-un transfer monetar urmat de jocul liber al schimbului de piață; dar banii lipsesc din cutia Edgeworth.
A doua teoremă fundamentală nu oferă un plan pentru îndreptarea relelor societății. Guvernul poate decide să realoce resursele între Octavio și Abby, mutându-le de la ω la α înainte de tranzacționarea zilei; și, în consecință, cine pierde poate decide să ia mai puțin pe piață a doua zi. A doua teoremă fundamentală nu ține cont de distorsiunile introduse de realocare.
Oferiți curbe
Curbele ofertei oferă un mijloc de a găsi puncte de echilibru și sunt utile și pentru investigarea existenței și unicității lor.
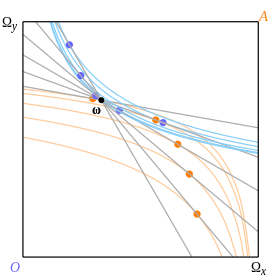
Două astfel de curbe, una pentru fiecare consumator și ambele în funcție de dotare, pot fi trasate în cutie. Pivotăm linia bugetară în jurul valorii de ω și trasăm cele mai favorizate puncte ale celor doi consumatori de-a lungul liniei, așa cum se arată în punctele colorate din Fig. 8. Acestea sunt puncte la care linia este tangențială la curbele lor de indiferență.
Locul punctelor cele mai favorizate ale consumatorului este curba ofertei sale. Fig. 9 arată curba ofertei lui Octavio ca albastru închis și Abby ca maro. Se întâlnesc în punctul ω ' și linia bugetară de echilibru (trasată în gri) este cea care trece prin acest punct. Curbele indiferenței prin ω ' pentru cei doi consumatori sunt prezentate în culori mai palide.
O curbă de ofertă trece în mod necesar prin punctul de dotare ω . Dacă îl luăm pe Abby ca exemplu, observăm că una dintre curbele ei de indiferență trebuie să treacă prin ω și că o linie bugetară poate fi aleasă pentru a avea același gradient ca și curba de indiferență aici, făcând din ω un punct cel mai favorizat pentru această linie.
În consecință, ofertele celor doi consumatori se intersectează neapărat la ω ; dar proprietatea care face ca acest lucru să se întâmple este că ω este singurul punct posibil de intersecție în concordanță cu liniile bugetare cu gradient diferit și, prin urmare, nu constituie neapărat un echilibru.
Orice intersecție a curbelor ofertei într-un alt punct decât ω determină un echilibru stabil. Dacă cele două curbe de ofertă sunt tangențiale la punctul de dotare, atunci acest punct este într-adevăr un echilibru și tangenta lor comună este linia bugetară corespunzătoare.
Terminologia pentru curbele ofertei
Curbele ofertei au fost utilizate pentru prima dată de Vilfredo Pareto - vezi Manuale / Manuel Chap. III, §97. El le-a numit „curbe de schimb” ( linee dei baratti / lignes des échanges ), iar numele său pentru alocarea preferată a lui Octavio de-a lungul unei linii bugetare a fost „punctul său de echilibru”.
Această alocare preferată este uneori denumită „cererea” lui Octavio, care constituie o descriere asimetrică a unui fapt simetric. O alocare determină participarea lui Abby la fel de mult ca a lui Octavio și, prin urmare, este la fel de mult o ofertă ca o cerere.
Offre este francez pentru „ofertă”, deci numirea unei curbe de ofertă un locus de cereri echivalează cu numirea unei curbe de ofertă un locus de cereri.
Unicitatea echilibrelor
S-ar putea presupune din considerații economice că, dacă există o tangentă comună printr-o anumită dotare și dacă curbele de indiferență nu sunt patologice în forma lor, atunci punctul de tangență va fi unic. Acest lucru se dovedește a nu fi adevărat. Condițiile pentru unicitatea echilibrului au făcut obiectul unor cercetări aprofundate: a se vedea teoria generală a echilibrului .
Fig. 9 și 10 ilustrează un exemplu din Mas-Colell și colab. în care trei echilibre distincte corespund punctului de înzestrare ω . Curbele indiferenței sunt:
(Octavio)
(Abby).
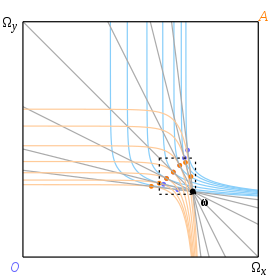
Curbele de indiferență umple caseta, dar sunt afișate numai atunci când sunt tangențiale unor linii bugetare reprezentative. Curbele ofertei, desenate în Fig. 11, se încrucișează în trei puncte prezentate de puncte gri mari și corespunzătoare cursurilor de schimb de 1 ⁄ 2 , 1 și 2.
Generalizări
Examinările timpurii ale proprietăților echilibrului s-au bazat pe o definiție implicită ca tangență, iar convexitatea pare a fi presupusă implicit. Nu exista nicio îndoială că echilibrul va fi atins: ascensiunea în gradient va duce la acesta. Dar rezultatele au lipsit de generalitate.
Echilibrele limită și curbele nediferențiate
Kenneth Arrow și Gérard Debreu au publicat lucrări în mod independent în 1951, atrăgând atenția asupra limitărilor din dovezile de calcul ale teoremelor de echilibru. Arrow a menționat în mod specific dificultatea cauzată de echilibrele la limită, iar Debreu problema curbelor de indiferență nediferențiate.
Fără a viza o acoperire exhaustivă, este ușor să vedem în termeni intuitivi cum să extindem metodele noastre pentru a aplica aceste cazuri. Trebuie să lărgim conceptul de tangentă pentru a include orice linie care atinge curba: o tangentă în sens etimologic mai degrabă decât cea a calculului diferențial. În exemplul din Fig. 12 există un arc de linii de preț legale printr-un punct de contact, fiecare atingând curbele de indiferență fără a le tăia în interiorul cutiei și, în consecință, există o gamă de echilibre posibile pentru o înzestrare dată.
Echilibru competitiv
Echilibrele din Fig. 12 nu sunt puncte în care curbele să fie adevărate tangente între ele. Cu toate acestea, ele au o proprietate care generalizează definiția în termeni de tangente, care este că cele două curbe pot fi separate local de o linie dreaptă.
Arrow și Debreu au definit echilibrul în același mod unul în celălalt în lucrările lor (independente) din 1951 fără a furniza nicio sursă sau raționament pentru definirea lor. Ei și-au păstrat definiția în lucrarea lor comună (despre existența echilibrului) din 1954. Noua definiție a necesitat o schimbare a tehnicii matematice de la calculul diferențial la teoria convexă a mulțimilor.
Definiția lor efectivă a fost aceasta: un echilibru realizabil dintr-o dotare ω constă dintr-o alocare x și o linie bugetară prin x și ω astfel încât să nu existe un punct de-a lungul liniei pe care fie consumatorul (strict) să îl prefere pe x . O pereche cuprinzând o alocare și o linie care satisface această proprietate este cunoscută sub numele de echilibru „Walrasian” sau „competitiv” .
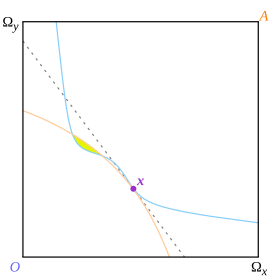
Linia bugetară a acestei definiții este o linie care separă curbele de indiferență ale celor doi consumatori, dar o face la nivel global, mai degrabă decât la nivel local. Arrow și Debreu nu explică de ce necesită separarea globală, ceea ce poate le-a ușurat dovezile, dar se poate vedea că are consecințe neașteptate. În Fig. 13, punctul x este un punct de tangență, care este, de asemenea, un punct în care curbele de indiferență sunt separate local de linia de preț punctată; dar deoarece acestea nu sunt separate la nivel global, punctul nu este un echilibru conform definiției lui Arrow și Debreu.
În Fig. 14 punctul x este un optim Pareto care nu satisface definiția echilibrului competitiv. Întrebarea dacă economia s-ar stabili într-un astfel de punct este destul de separată de dacă satisface o definiție dată a echilibrului; evident, în acest caz, s-ar stabili într-adevăr acolo.
Arrow și Debreu au inclus întotdeauna convexitatea curbelor de indiferență printre „presupunerile” lor. Termenul „presupuneri” este unul vag care s-ar putea referi la o presupoziție care stă la baza definițiilor, precum și la teoreme, sau la o premisă care este necesară doar pentru acestea din urmă. Având în vedere că definiția lor nu include toate echilibrele care pot exista atunci când curbele pot fi neconvexe, este posibil să fi însemnat asumarea convexității în sensul anterior. Indiferent dacă acest lucru este sau nu, definiția a fost adoptată pe scară largă, fără nicio restricție a domeniului.
Uneori s-a constatat că rezultatele pot fi obținute sub definiția lor fără a presupune convexitate în dovadă (prima teoremă fundamentală a economiei bunăstării fiind un exemplu).
Existența echilibrului competitiv
În unele economii nu va exista un punct de odihnă care să poată fi atins dintr-o anumită dotare prin schimb la prețuri uniforme; prin urmare, nu există un punct de odihnă care să satisfacă definiția echilibrului competitiv. Familiile de curbe ale modelului din Fig. 14 sunt un exemplu în acest sens.
Teoremele fundamentale ale economiei bunăstării
Cu echilibrul definit ca „echilibru competitiv”, prima teoremă fundamentală poate fi demonstrată chiar dacă curbele de indiferență nu trebuie să fie convexe: orice echilibru competitiv este (global) Pareto optim. Cu toate acestea, dovada nu mai este evidentă, iar cititorul este trimis la articolul despre teoremele fundamentale ale economiei bunăstării .
Nu s-ar fi considerat că același rezultat se menține (cu curbe de indiferență neconvexe) sub definiția tangenței echilibrului. Punctul x din Fig. 13 ar fi fost considerat un echilibru care nu a fost (global) optim deoarece regiunea galbenă Pareto îl domină.
Nu rezultă că rezultatul a fost consolidat, deoarece realizarea echilibrului a fost făcută îndoielnică. În Fig. 13, punctul x poate să nu fie un „echilibru competitiv”, dar economia se poate bloca acolo împiedicându-l să atingă echilibrul „adevărat” (și optim Pareto) în regiunea galbenă.
Întotdeauna a fost considerat esențial pentru prima teoremă a bunăstării că echilibrul ar fi de fapt atins. Interpretarea teoremei de către Lerner a fost că „Din fericire, alocarea optimă a bunurilor poate fi atinsă automat”. Cu toate acestea, nimic nu poate garanta că un optim global va fi atins atunci când optima locală este prezentă. Dacă conceptul de echilibru include optime locale cum ar fi x , atunci echilibrul poate fi atins, dar sub-optim; dacă astfel de puncte sunt excluse, atunci echilibrul poate fi optim, dar de neatins.
Diferențele cauzate de neconvexitate devin mai adânc înrădăcinate atunci când ne uităm la a doua teoremă fundamentală. Nu fiecare optim Pareto este un echilibru competitiv (deși poate fi totuși un loc de odihnă pentru economie). În consecință, teorema trebuie fie să li se ofere convexitatea preferințelor ca premisă, fie să se afirme în așa fel încât „echilibrul” să nu fie înțeles ca „echilibru competitiv” așa cum s-a definit mai sus.
Note
Referințe
- Mas-Colell, Andreu ; Whinston, Michael D .; Jerry R. Green (1995). Teoria microeconomică . New York: Oxford University Press. ISBN 0-19-507340-1.
- Vilfredo Pareto , Manuale di Economia Politica con una Introduzione alla Scienza Sociale (1906) / Manuel d'Économie Politique (1909) (efectiv o a doua ediție a versiunii italiene), Eng. tr. (al francezilor) ca „Manual de economie politică” (1971). Textul în italiană este disponibil online la https://archive.org/details/manualedieconomi00pareuoft .