Arborele de întindere minim euclidian -Euclidean minimum spanning tree

Un arbore de întindere minim euclidian al unui set finit de puncte în planul euclidian sau spațiul euclidian de dimensiuni mai mari conectează punctele printr-un sistem de segmente de linie cu punctele ca puncte finale, minimizând lungimea totală a segmentelor. În ea, oricare două puncte pot ajunge unul la celălalt de-a lungul unei căi prin segmentele de linie. Poate fi găsit ca arborele de acoperire minim al unui grafic complet cu punctele ca vârfuri și distanțele euclidiene dintre puncte ca greutăți de margine.

Marginile arborelui care se întinde minim se întâlnesc la unghiuri de cel puțin 60°, cel mult șase până la un vârf. La dimensiuni mai mari, numărul de muchii pe vârf este delimitat de numărul de sfere unitare tangente . Lungimea totală a marginilor, pentru punctele dintr-un pătrat unitar , este cel mult proporțională cu rădăcina pătrată a numărului de puncte. Fiecare muchie se află într-o regiune goală a planului, iar aceste regiuni pot fi folosite pentru a demonstra că arborele de acoperire minim euclidian este un subgraf al altor grafice geometrice , inclusiv graficul de vecinătate relativă și triangulația Delaunay . Construind triangulația Delaunay și apoi aplicând un algoritm de arbore de întindere minim de grafic, arborele de întindere minim al punctelor plane date poate fi găsit în timp , așa cum este exprimat în notația O mare . Acest lucru este optim în unele modele de calcul, deși există algoritmi randomizați mai rapid pentru puncte cu coordonate întregi. Pentru punctele de dimensiuni mai mari, găsirea unui algoritm optim rămâne o problemă deschisă . ${\displaystyle n}$${\displaystyle O(n\log n)}$

Definiție și probleme conexe

Un arbore de acoperire minim euclidian, pentru o mulțime de puncte din planul euclidian sau spațiul euclidian , este un sistem de segmente de linie , având ca puncte finale numai punctele date, a cărui unire include toate punctele dintr-o mulțime conexă și care are lungimea totală minimă posibilă a oricărui astfel de sistem. O astfel de rețea nu poate conține un inel poligonal de segmente; dacă ar exista una, rețeaua ar putea fi scurtată prin eliminarea unei margini a poligonului. Prin urmare, rețeaua de lungime minimă formează un arbore . Această observație conduce la definiția echivalentă că un arbore de întindere minim euclidian este un arbore de segmente de linie între perechi de puncte date, de lungime totală minimă. Același arbore poate fi, de asemenea, descris ca un arbore de întindere minim al unui grafic complet ponderat , având punctele date ca vârfuri și distanțele dintre puncte ca greutăți de margine. Aceleași puncte pot avea mai mult de un arbore de întindere minim. De exemplu, pentru vârfurile unui poligon obișnuit , eliminarea oricărei margini a poligonului produce un arbore de întindere minim. ${\displaystyle n}$

Publicațiile despre arborele de întindere minim euclidian îl abrevierează în mod obișnuit ca „EMST”. Ele pot fi, de asemenea, numiți „arbori de întindere minim geometric”, dar acest termen poate fi folosit mai general pentru spații geometrice cu distanțe non-euclidiene, cum ar fi spațiile L ^p . Când contextul seturilor de puncte euclidiene este clar, ele pot fi numite pur și simplu „arbori de întindere minimă”.

Câteva alte rețele geometrice standard sunt strâns legate de arborele de acoperire minim euclidian:

• Problema arborelui Steiner caută din nou un sistem de segmente de linie care să conecteze toate punctele date, dar fără a necesita ca segmentele să înceapă și să se termine doar în punctele date. În această problemă, pot fi adăugate puncte suplimentare ca puncte finale ale segmentului, permițând arborelui Steiner să fie mai scurt decât arborele de întindere minim.
• În problema căii euclidiane ale vânzătorului ambulant , segmentele de linie de legătură trebuie să înceapă și să se termine în punctele date, precum arborele care se întinde și spre deosebire de arborele Steiner; în plus, fiecare punct poate atinge cel mult două segmente de linie, astfel încât rezultatul formează un lanț poligonal . Din cauza acestei restricții, calea optimă poate fi mai lungă decât arborele de întindere minim euclidian, dar este de cel mult de două ori mai lungă.
• Cheile geometrice sunt rețele cu greutate redusă care, la fel ca arborele de întindere minim, conectează toate punctele. Spre deosebire de arborele de întindere minim, toate aceste căi de legătură trebuie să fie scurte, având lungime proporțională cu distanța dintre punctele pe care le conectează. Pentru a atinge această proprietate, aceste rețele au în general cicluri și deci nu sunt copaci.

Proprietăți

Unghiuri și grade de vârf

Ori de câte ori două muchii ale unui arbore de întindere minim euclidian se întâlnesc la un vârf, ele trebuie să formeze un unghi de 60° sau mai mult, cu egalitate numai atunci când formează două laturi ale unui triunghi echilateral . Acest lucru se datorează faptului că, pentru două margini care formează orice unghi mai ascuțit, una dintre cele două margini ar putea fi înlocuită cu a treia margine, mai scurtă, a triunghiului pe care îl formează, formând un copac cu lungimea totală mai mică. În comparație, problema arborelui Steiner are un unghi mai puternic: un arbore Steiner optim are toate unghiurile de cel puțin 120°.

Aceeași limită de unghi de 60° apare și în problema numărului de sărut , de găsire a numărului maxim de sfere unitare în spațiul euclidian care pot fi tangente la o sferă unitate centrală fără să se intersecteze două sfere (dincolo de un punct de tangență). Punctele centrale ale acestor sfere au un arbore care se întinde minim sub forma unei stele , cu punctul central adiacent tuturor celorlalte puncte. Dimpotrivă, pentru orice vârf al oricărui arbore care se întinde minim, se pot construi sfere unitare care nu se suprapun, centrate în și în puncte, două unități de-a lungul fiecărei margini, cu o tangență pentru fiecare vecin de . Prin urmare, în spațiul dimensional, gradul maxim posibil al unui vârf (numărul de margini ale arborelui care se întind conectate la acesta) este egal cu numărul de sfere în dimensiuni. Arborii de întindere minim planar au gradul de cel mult șase, iar când un copac are gradul șase, există întotdeauna un alt arbore de întindere minim cu gradul maxim cinci. Arborii tridimensionali care se întind minim au gradul de cel mult doisprezece. Singurele dimensiuni mai mari în care se cunoaște valoarea exactă a numărului săruturilor sunt patru, opt și 24 de dimensiuni. ${\displaystyle v}$${\displaystyle v}$${\displaystyle v}$${\displaystyle n}$${\displaystyle n}$

Pentru punctele generate la întâmplare dintr-o distribuție continuă dată, arborele de acoperire minim este aproape sigur unic. Numărul de vârfuri de orice grad dat converg, pentru un număr mare de vârfuri, la o constantă înmulțită cu acel număr de vârfuri. Valorile acestor constante depind de grad și de distribuție. Cu toate acestea, chiar și pentru cazuri simple - cum ar fi numărul de frunze pentru puncte distribuite uniform într-un pătrat unitar - valorile lor precise nu sunt cunoscute.

Regiuni goale

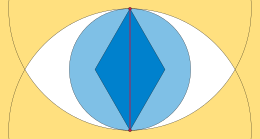
Pentru orice margine a oricărui arbore de întindere minim euclidian, lentila (sau vesica piscis ) formată prin intersectarea celor două cercuri cu ca raze ale lor nu poate avea niciun alt vârf dat în interiorul său. Altfel spus, dacă orice copac are o margine a cărei lentilă conține un al treilea punct , atunci nu are lungimea minimă. Căci, prin geometria celor două cercuri, ar fi mai aproape de amândoi și decât sunt unul de celălalt. Dacă marginea ar fi îndepărtată din copac, ar rămâne conectată la unul dintre și , dar nu și la celălalt. Înlocuirea marginii eliminate cu sau (oricare dintre aceste două margini se reconecta la vârful de la care a fost deconectată) ar produce un arbore mai scurt. ${\displaystyle uv}$${\displaystyle uv}$${\displaystyle w}$${\displaystyle uv}$${\displaystyle w}$${\displaystyle w}$${\displaystyle u}$${\displaystyle v}$${\displaystyle uv}$${\displaystyle w}$${\displaystyle u}$${\displaystyle v}$${\displaystyle uv}$${\displaystyle uw}$${\displaystyle vw}$${\displaystyle w}$

Pentru orice margine a oricărui arbore de întindere minim euclidian, rombul cu unghiuri de 60° și 120°, având drept diagonală lungă, este disjuns de romburile formate în mod analog de toate celelalte margini. Două muchii care împărtășesc un punct de capăt nu pot avea rombi suprapusi, deoarece asta ar implica un unghi de margine mai ascuțit de 60°, iar două muchii disjunse nu pot avea rombi suprapusi; dacă au făcut-o, cea mai lungă dintre cele două muchii ar putea fi înlocuită cu o muchie mai scurtă între aceleași patru vârfuri. ${\displaystyle uv}$${\displaystyle uv}$

Supergrafe

Anumite grafice geometrice au definiții care implică regiuni goale în seturi de puncte, din care rezultă că acestea conțin fiecare muchie care poate face parte dintr-un arbore de acoperire minim euclidian. Acestea includ:

• Graficul de vecinătate relativă , care are o margine între orice pereche de puncte ori de câte ori lentila pe care o definesc este goală.
• Graficul Gabriel , care are o muchie între orice pereche de puncte ori de câte ori cercul având perechea ca diametru este gol.
• Triangulația Delaunay , care are o margine între orice pereche de puncte ori de câte ori există un cerc gol având perechea ca coardă.
• Graficul Urquhart , format din triangulația Delaunay prin eliminarea marginii celei mai lungi a fiecărui triunghi. Pentru fiecare muchie rămasă, vârfurile triunghiurilor Delaunay care folosesc acea muchie nu se pot afla în luna goală a graficului de vecinătate relativă.

Deoarece criteriile de regiune goală pentru aceste grafice sunt progresiv mai slabe, aceste grafice formează o secvență ordonată de subgrafe. Adică, folosind „⊆” pentru a desemna relația de submulțime dintre marginile lor, aceste grafice au relațiile:

Un alt grafic garantat pentru a conține arborele de întindere minim este graficul Yao , determinat pentru punctele din plan prin împărțirea planului din jurul fiecărui punct în șase pene de 60° și conectând fiecare punct la cel mai apropiat vecin din fiecare pană. Graficul rezultat conține graficul de vecinătate relativă, deoarece două vârfuri cu o lentilă goală trebuie să fie cele mai apropiate vecine unul de celălalt în pene. Ca și în cazul multor dintre celelalte grafice geometrice de mai sus, această definiție poate fi generalizată la dimensiuni mai mari și (spre deosebire de triangulația Delaunay) generalizările sale includ întotdeauna un număr liniar de muchii.

Lungime totală

Pentru punctele din pătratul unității (sau orice altă formă fixă), lungimea totală a marginilor minime ale arborelui este de . Unele seturi de puncte, cum ar fi punctele dispuse uniform într-o grilă, ating această limită. Pentru punctele dintr-un hipercub unitar în spațiul -dimensional, limita corespunzătoare este . Aceeași limită se aplică și lungimii totale așteptate a arborelui de acoperire minim pentru punctele alese uniform și independent de un pătrat unitar sau un hipercub unitar. Revenind la pătratul unității, suma pătratului lungimii muchiilor arborelui de întindere minim este . Această limită rezultă din observația că marginile au rombi disjunși, cu aria proporțională cu lungimile marginilor la pătrat. Limita lungimii totale urmează prin aplicarea inegalității Cauchy-Schwarz . ${\displaystyle n}$${\displaystyle O({\sqrt {n}})}$${\displaystyle {\sqrt {n}}\times {\sqrt {n}}}$${\displaystyle d}$${\displaystyle O(n^{(d-1)/d})}$${\displaystyle n}$${\displaystyle O(1)}$${\displaystyle O({\sqrt {n}})}$

O altă interpretare a acestor rezultate este că lungimea medie a muchiei pentru orice set de puncte dintr-un pătrat unitar este , cel mult proporțională cu distanța dintre punctele dintr-o grilă obișnuită; și că pentru puncte aleatoare dintr-un pătrat unitar lungimea medie este proporțională cu . Cu toate acestea, în cazul aleatoriu, cu mare probabilitate muchia cea mai lungă are lungimea aproximativă${\displaystyle O(1/{\sqrt {n}})}$${\displaystyle 1/{\sqrt {n}}}$

mai mult decât media cu un factor non-constant. Cu mare probabilitate, cea mai lungă margine formează o frunză a arborelui care se întinde și conectează un punct departe de toate celelalte puncte cu cel mai apropiat vecin. Pentru un număr mare de puncte, distribuția lungimii celei mai lungi muchii în jurul valorii sale așteptate converge către o distribuție Laplace .

Orice cheie geometrică , un subgraf al unui grafic geometric complet ale cărui trasee cele mai scurte se aproximează la distanța euclidiană, trebuie să aibă lungimea totală a muchiei cel puțin la fel de mare ca arborele de întindere minim, iar una dintre măsurile standard de calitate pentru o cheie geometrică este raportul dintre lungimea totală și a arborelui spanning minim pentru aceleași puncte. Mai multe metode de construire a cheilor, cum ar fi cheia geometrică lacomă , realizează o limită constantă pentru acest raport. S-a presupus că raportul Steiner , cel mai mare raport posibil dintre lungimea totală a unui arbore care se întinde minim și arborele Steiner pentru același set de puncte din plan, este raportul pentru trei puncte dintr-un triunghi echilateral . ${\displaystyle 2/{\sqrt {3}}\aproximativ 1,1547}$

Subdiviziune

Dacă fiecare margine a unui arbore de întindere minim euclidian este subdivizată, prin adăugarea unui nou punct la mijlocul său, atunci arborele rezultat este totuși un arbore de întindere minim al setului de puncte augmentat. Repetarea acestui proces de subdiviziune permite ca un arbore de acoperire minim euclidian să fie subdivizat arbitrar fin. Cu toate acestea, subdivizarea doar a unora dintre muchii sau subdivizarea muchiilor în alte puncte decât punctul de mijloc, poate produce un set de puncte pentru care arborele subdivizat nu este arborele de acoperire minim.

Complexitatea computațională

Pentru puncte din orice dimensiune, arborele de întindere minim poate fi construit în timp prin construirea unui grafic complet cu o muchie între fiecare pereche de puncte, ponderat cu distanța euclidiană și apoi aplicând un algoritm de arbore de întindere minim pentru grafic, cum ar fi Prim–Dijkstra– Algoritmul Jarník sau algoritmul lui Borůvka pe el. Acești algoritmi pot fi făcuți să ia timp pe grafice complete, spre deosebire de o altă alegere comună, algoritmul lui Kruskal , care este mai lent deoarece implică sortarea tuturor distanțelor. Pentru punctele din spații cu dimensiuni reduse, problema poate fi rezolvată mai rapid, așa cum este detaliat mai jos. ${\displaystyle O(n^{2})}$${\displaystyle O(n^{2})}$

Calcularea distanțelor euclidiene implică un calcul al rădăcinii pătrate . În orice comparație a greutăților marginilor, compararea pătratelor distanțelor euclidiene, în locul distanțelor în sine, dă aceeași ordine și, prin urmare, nu schimbă restul calculului arborelui. Această comandă rapidă accelerează calculul și permite construirea unui arbore de acoperire minim pentru puncte cu coordonate întregi folosind numai aritmetica întregi.

Două dimensiuni

O abordare mai rapidă a găsirii arborelui de acoperire minim al punctelor plane utilizează proprietatea că este un subgraf al triangulației Delaunay:

1. Calculați triangulația Delaunay, care poate fi făcută în timp. Deoarece triangulația Delaunay este un graf plan , are cel mult muchii.${\displaystyle O(n\log n)}$${\displaystyle 3n-6}$
2. Etichetați fiecare margine cu lungimea ei (pătratată).
3. Rulați un algoritm de arbore de întindere minim pentru grafic. Deoarece există margini, acest lucru necesită timp folosind oricare dintre algoritmii standard de arbore de acoperire minim.${\displaystyle O(n)}$${\displaystyle O(n\log n)}$

Rezultatul este un algoritm care necesită timp, optim în anumite modele de calcul (vezi mai jos ). ${\displaystyle O(n\log n)}$

Dacă coordonatele de intrare sunt numere întregi și pot fi utilizate ca indici de matrice , sunt posibili algoritmi mai rapizi: triangulația Delaunay poate fi construită printr-un algoritm randomizat în timpul așteptat. În plus, deoarece triangulația Delaunay este un graf plan , arborele său de acoperire minim poate fi găsit în timp liniar printr-o variantă a algoritmului lui Borůvka care elimină toate marginile, cu excepția celei mai ieftine, dintre fiecare pereche de componente după fiecare etapă a algoritmului. Prin urmare, timpul total așteptat pentru acest algoritm este . În cealaltă direcție, triangulația Delaunay poate fi construită din arborele de acoperire minim în limita de timp aproape liniară , unde denotă logaritmul iterat . ${\displaystyle O(n\log \log n)}$${\displaystyle O(n\log \log n)}$${\displaystyle O(n\log ^{*}n)}$${\displaystyle \log ^{*}}$

Dimensiuni mai mari

Problema poate fi generalizată și la puncte din spațiul -dimensional . În dimensiuni mai mari, conectivitatea determinată de triangulația Delaunay (care, la fel, împarte corpul convex în simplexe dimensionale ) conține arborele de întindere minim; totuși, triangulația poate conține graficul complet. Prin urmare, găsirea arborelui spanning euclidian minim ca arbore spanning al graficului complet sau ca arbore spanning al triangulației Delaunay necesită timp. Pentru trei dimensiuni arborele de întindere minim poate fi găsit în timp , iar în orice dimensiune mai mare, în timp ${\displaystyle n}$${\displaystyle d}$${\displaystyle \mathbb {R} ^{d}}$${\displaystyle d}$${\displaystyle O(dn^{2})}$${\displaystyle O{\bigl (}(n\log n)^{4/3}{\bigr )}}$

pentru orice — mai rapid decât limita de timp pătratică pentru graficul complet și algoritmii de triangulație Delaunay. ${\displaystyle \varepsilon >0}$

Complexitatea optimă a timpului pentru arbori de întindere minim de dimensiuni mai mari rămâne necunoscută, dar este strâns legată de complexitatea calculării perechilor bicromatice cele mai apropiate . În problema perechii celei mai apropiate bicromatice, intrarea este un set de puncte, având două culori diferite (să zicem, roșu și albastru). Ieșirea este o pereche de un punct roșu și un punct albastru cu distanța minimă posibilă. Această pereche formează întotdeauna una dintre marginile arborelui care se întinde minim. Prin urmare, problema perechii celei mai apropiate bicromatice poate fi rezolvată în timpul necesar pentru a construi un arbore care se întinde minim și a-i scana marginile pentru cea mai scurtă margine roșu-albastru. Dimpotrivă, pentru orice colorare roșu-albastru a oricărui subset al unui set dat de puncte, perechea cea mai apropiată bicromatică produce o margine a arborelui de acoperire minim al submulțimii. Prin alegerea cu atenție a unei secvențe de colorații a submulților și găsirea celei mai apropiate perechi bicromatice a fiecărei subprobleme, arborele de acoperire minim poate fi găsit în timp proporțional cu timpul optim pentru găsirea perechilor bicromatice cele mai apropiate pentru același număr de puncte, indiferent de momentul optim. se dovedește a fi.

Pentru seturi de puncte uniform aleatoare în orice dimensiune mărginită, graficul Yao sau triangulația Delaunay au un număr liniar așteptat de muchii, este garantat să conțină arborele de întindere minim și poate fi construit în timpul așteptat liniar. Din aceste grafice, arborele de întindere minim în sine poate fi construit în timp liniar, utilizând un algoritm de timp liniar randomizat pentru arbori de întindere minim de grafic . Cu toate acestea, performanța slabă a acestor metode asupra intrărilor care provin din date grupate i-a determinat pe cercetătorii de inginerie algoritmică să dezvolte metode cu o limită de timp oarecum mai lentă, pentru intrări aleatorii sau intrări ale căror distanțe și grupări seamănă cu cele ale datelor aleatoare, prezentând în același timp performanțe mai bune pe real. - date despre lume. ${\displaystyle O(n\log n)}$

O descompunere de perechi bine separată este o familie de perechi de submulțimi ale punctelor date, astfel încât fiecare pereche de puncte să aparțină uneia dintre aceste perechi de submulțimi și astfel încât toate perechile de puncte care provin din aceeași pereche de submulțimi au aproximativ aceeasi lungime. Este posibil să se găsească o descompunere de perechi bine separată cu un număr liniar de submulțimi și o pereche reprezentativă de puncte pentru fiecare submulțime, în timp . Arborele de acoperire minim al graficului format din aceste perechi reprezentative este apoi o aproximare a arborelui de acoperire minim. Folosind aceste idei, o aproximare a arborelui de acoperire minim poate fi găsită în timp, pentru constantă . Mai precis, prin alegerea fiecărei perechi reprezentative pentru a aproxima perechea cea mai apropiată din clasa sa de echivalență și variind cu atenție calitatea acestei aproximări pentru diferite perechi, dependența în limita de timp poate fi dată ca pentru orice dimensiune fixă. ${\displaystyle O(n\log n)}$${\displaystyle (1+\varepsilon )}$${\displaystyle O(n\log n)}$${\displaystyle \varepsilon }$${\displaystyle \varepsilon }$${\displaystyle O(n\log n+(\varepsilon ^{-2}\log ^{2}{\tfrac {1}{\varepsilon }})n),}$

Dinamic și cinetic

Arborele de acoperire minim euclidian a fost generalizat în multe moduri diferite la sistemele de mișcare sau schimbare a punctelor:

• Dacă un set de puncte suferă o succesiune de inserții sau ștergeri dinamice de puncte, fiecare dintre aceste actualizări induce o cantitate limitată de modificare a arborelui de acoperire minim al punctelor. Când secvența de actualizare este cunoscută dinainte, pentru punctele din plan, modificarea după fiecare inserare sau ștergere poate fi găsită în timp pentru fiecare inserare sau ștergere. Când actualizările trebuie gestionate online , se cunoaște o limită de timp mai lentă (dar totuși polilogaritmică) . Pentru versiunile cu dimensiuni mai mari ale problemei, timpul per actualizare este mai lent, dar tot subliniar.${\displaystyle O(\log ^{2}n)}$${\displaystyle O(\log ^{10}n)}$
• Pentru punctele care se deplasează liniar cu viteză constantă sau cu mișcări algebrice mai generale, arborele de întindere minim se va schimba printr-o succesiune de schimburi, în care o muchie este îndepărtată și alta o înlocuiește într-un moment în care ambele au lungime egală. Pentru mișcările liniare, numărul de modificări este cel mult puțin mai mare decât . Pentru mișcările algebrice mai generale, există o limită superioară aproape cubică a numărului de schimburi, bazată pe teoria secvențelor Davenport-Schinzel .${\displaystyle n}$${\displaystyle n^{25/9}}$
• Problema arborelui care se întinde în mișcare minimă se referă din nou la punctele care se mișcă liniar cu viteză constantă, pe un interval de timp, și caută un singur arbore care minimizează suma maximă a greutăților care apar în orice moment în acest interval. Este NP-greu de calculat exact, dar poate fi aproximat cu un factor de doi în timp polinomial.
• Problema arborelui de întindere minim euclidian cinetic cere o structură de date cinetice care să poată menține arborele de întindere minim pe măsură ce punctele sale suferă atât mișcări continue, cât și inserții și ștergeri. Mai multe lucrări au studiat astfel de structuri și este cunoscută o structură cinetică pentru puncte în mișcare algebrică cu timp total aproape cubic, care se potrivește aproape cu limita numărului de schimburi.

Limita inferioară

O limită inferioară asimptotică a problemei arborelui de acoperire minim euclidian poate fi stabilită în modele restrânse de calcul. Acestea includ arborele de decizie algebric și modelele arbore de calcul algebric , în care algoritmul are acces la punctele de intrare numai prin anumite primitive restricționate care efectuează calcule algebrice simple pe coordonatele lor. În aceste modele, problema celei mai apropiate perechi de puncte necesită timp, dar cea mai apropiată pereche este în mod necesar o margine a arborelui de întindere minimă, astfel încât arborele de întindere minim necesită și acest timp. Prin urmare, algoritmii pentru construirea arborelui de acoperire minim planar în timp în cadrul acestui model, de exemplu prin utilizarea triangulației Delaunay, sunt optimi. Cu toate acestea, aceste limite inferioare nu se aplică modelelor de calcul cu coordonate punct întreg, în care sunt permise operații pe biți și operațiuni de indexare a tabelelor pe acele coordonate. În aceste modele, sunt posibili algoritmi mai rapizi, așa cum este descris mai sus. ${\displaystyle \Omega (n\log n)}$${\displaystyle \Omega (n\log n)}$${\displaystyle O(n\log n)}$

Aplicații

O aplicație evidentă a arborilor de întindere minim euclidien este găsirea celei mai ieftine rețele de fire sau conducte pentru a conecta un set de locuri, presupunând că legăturile costă o sumă fixă ​​pe unitate de lungime. Primele publicații despre arbori cu întindere minimă au vizat, în general, o versiune geografică a problemei, care implică proiectarea unei rețele electrice pentru sudul Moraviei , iar o aplicație pentru minimizarea lungimii firelor în circuite a fost descrisă în 1957 de Loberman și Weinberger.

Arborele de acoperire minimă sunt strâns legate de gruparea cu o singură legătură , una dintre mai multe metode de grupare ierarhică . Marginile unui arbore de întindere minim, sortate după lungimea lor, dau ordinea în care se îmbină clusterele în clustere mai mari în această metodă de grupare. Odată ce aceste muchii au fost găsite, prin orice algoritm, ele pot fi utilizate pentru a construi gruparea cu o singură legătură în timp . Deși formele lungi și subțiri ale clusterelor produse prin clustering cu o singură legătură pot fi o potrivire proastă pentru anumite tipuri de date, cum ar fi amestecurile de distribuții gaussiene , poate fi o alegere bună în aplicațiile în care clusterele în sine sunt de așteptat să aibă forme lungi și subțiri. cum ar fi în modelarea halourilor de materie întunecată din galaxii . În știința informațiilor geografice , mai multe grupuri de cercetători au folosit arbori care se întind minim ai centroizilor clădirilor pentru a identifica grupuri semnificative de clădiri, de exemplu prin eliminarea marginilor identificate într-un alt mod ca fiind inconsistente. ${\displaystyle O(n\log n)}$

Arborele de întindere minimă au fost, de asemenea, folosiți pentru a deduce forma curbelor în plan, date fiind punctele eșantionate de-a lungul curbei. Pentru o curbă netedă, eșantionată mai fin decât dimensiunea caracteristică locală , arborele de întindere minim va forma o cale care conectează puncte consecutive de-a lungul curbei. În general, metode similare pot recunoaște curbele desenate într-un stil punctat sau punctat, mai degrabă decât ca un singur set conectat. Aplicațiile acestei tehnici de găsire a curbei includ fizica particulelor , în identificarea automată a urmelor lăsate de particule într-o cameră cu bule . Versiunile mai sofisticate ale acestei idei pot găsi curbe dintr-un nor de puncte de eșantionare zgomotoase care urmează aproximativ conturul curbei, folosind topologia arborelui care se întinde pentru a ghida metoda celor mai mici pătrate în mișcare .

O altă aplicație a arborilor de întindere minimă este un algoritm de aproximare cu factor constant pentru problema euclidiană a vânzătorului ambulant , problema găsirii celei mai scurte poligonalizări a unui set de puncte. Plimbarea în jurul limitei arborelui care se întinde minim poate aproxima turul optim al vânzătorului călător într-un factor de doi din lungimea optimă. Cu toate acestea, schemele de aproximare în timp polinomial mai precise sunt cunoscute pentru această problemă. În rețelele ad-hoc fără fir , difuzarea mesajelor de-a lungul căilor într-un arbore de întindere minim poate fi o aproximare precisă a rutare de difuzare cu energie minimă, care este, din nou, greu de calculat exact.

Realizare

Problema de realizare pentru arborii de întindere minim euclidieni ia ca intrare un arbore abstract și caută o locație geometrică pentru fiecare vârf al arborelui (într-un spațiu de o dimensiune fixă), astfel încât arborele dat să fie egal cu arborele de întindere minim al acelor puncte. Nu orice copac abstract are o astfel de realizare; de exemplu, arborele trebuie să respecte numărul de sărut legat de gradul fiecărui vârf. Există restricții suplimentare; de exemplu, nu este posibil ca un arbore de întindere minim plan să aibă un vârf de gradul șase adiacent unui vârf de gradul cinci sau șase. Determinarea dacă există o realizare bidimensională este NP-hard . Totuși, dovada durității depinde de faptul că vârfurile de gradul șase dintr-un arbore au un set foarte restrâns de realizări: vecinii unui astfel de vârf trebuie plasați pe vârfurile unui hexagon regulat centrat pe acel vârf. Într-adevăr, pentru arborii de gradul maxim cinci, o realizare plană există întotdeauna. În mod similar, pentru arborii de gradul maxim zece, există întotdeauna o realizare tridimensională. Pentru aceste realizări, unii copaci pot necesita margini de lungime exponențială și casete de delimitare cu suprafață exponențială în raport cu lungimea marginii lor celei mai scurte. Arborii de gradul maxim patru au realizări plane mai mici, cu lungimi de margine delimitate polinomial și casete de delimitare.

Vezi si

• Arborele de întindere minim rectiliniu , un arbore de întindere minim cu distanțe măsurate folosind geometria taxiului

Referințe

linkuri externe

• Tutorial EMST , documentație mlpack