Teorema celor trei geodezii - Theorem of the three geodesics
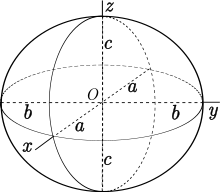
În geometria diferențială , teorema celor trei geodezii , cunoscută și sub numele de teorema Lyusternik – Schnirelmann , afirmă că fiecare varietate riemanniană cu topologia unei sfere are cel puțin trei geodezii închise care formează curbe închise simple (adică fără auto-intersecții). Rezultatul poate fi extins și la cvasigeodezice pe un poliedru convex. Teorema este ascuțită: deși fiecare sferă riemanniană 2 conține infinit de multe geodezii închise distincte, doar trei dintre ele sunt garantate să nu aibă intersecții de sine. De exemplu, printr-un rezultat al lui Morse, dacă lungimile a 3 axe principale ale unui elipsoid sunt distincte, dar suficient de apropiate unele de altele, atunci elipsoidul are doar 3 geodezii închise simple.
Istorie și dovadă
O geodezică , pe o suprafață riemanniană, este o curbă care este locală drept în fiecare dintre punctele sale. De exemplu, pe planul euclidian geodezice sunt linii , iar pe suprafața unei sfere geodezice sunt cercuri mari . Cea mai scurtă cale din suprafața dintre două puncte este întotdeauna geodezică, dar pot exista și alte geodezice. Se spune că o geodezică este o geodezică închisă dacă revine la punctul său de pornire și direcția de plecare; procedând astfel, se poate încrucișa de mai multe ori. Teorema celor trei geodezii spune că pentru suprafețele homeomorfe ale sferei, există cel puțin trei geodezii închise care nu se auto-traversează. Pot fi mai mult de trei, de exemplu, sfera în sine are infinit de multe.
Acest rezultat provine din matematica navigației oceanice, unde suprafața pământului poate fi modelată cu precizie de un elipsoid și din studiul geodeziei pe un elipsoid , cele mai scurte căi pe care navele le pot parcurge. În special, un elipsoid triaxial aproape sferic are doar trei elemente geodezice închise simple, ecuatoarele sale. În 1905, Henri Poincaré a conjecturat că fiecare suprafață netedă echivalent topologic cu o sferă conține, de asemenea, cel puțin trei simple geodezii închise, iar în 1929 Lazar Lyusternik și Lev Schnirelmann au publicat o dovadă a conjecturii, care s-a dovedit ulterior că este defectă. Dovada a fost reparată de Hans Werner Ballmann în 1978.
O dovadă a acestei conjecturi examinează omologia spațiului curbelor netede pe sferă și folosește fluxul de scurtare a curbelor pentru a găsi o geodezică simplă închisă care reprezintă fiecare dintre cele trei clase de omologie nontriviale ale acestui spațiu.
Generalizări
O versiune consolidată a teoremei afirmă că, pe orice suprafață riemanniană care este topologic o sferă, există neapărat trei geodezii închise simple a căror lungime este cel mult proporțională cu diametrul suprafeței.
Numărul de lungimi geodezice închise de cel mult L pe o sferă topologică netedă crește proporțional cu L / log L , dar nu se poate garanta că toate aceste geodezii sunt simple.
Pe suprafețele Riemann hiperbolice compacte , există infinit multe geodezii închise simple, dar numai finit multe cu o lungime dată legată. Acestea sunt codificate analitic de funcția zeta Selberg . Rata de creștere a numărului de geodezice simple închise, în funcție de lungimea lor, a fost investigată de Maryam Mirzakhani .
Valori neuniforme
Există un algoritm care poate găsi un quasigeodesic închis simplu pe un poliedru convex în timp polinomial?
De asemenea, este posibil să se definească geodezice pe unele suprafețe care nu sunt netede peste tot, cum ar fi poliedrele convexe . Suprafața unui poliedru convex are o metrică care este local euclidiană, cu excepția vârfurilor poliedrului, iar o curbă care evită vârfurile este geodezică dacă urmărește segmente de linie dreaptă în fiecare față a poliedrului și rămâne drept peste fiecare margine a poliedrului că traversează. Deși unele poliedre au geodezice închise simple (de exemplu, tetraedrul obișnuit și defenoidele au infinit de multe geodezice închise, toate simple) altele nu. În special, o simplă geodezică închisă a unui poliedru convex ar bisecta neapărat defectul unghiular total al vârfurilor și aproape toate poliedrele nu au astfel de bisectoare.
Cu toate acestea, teorema celor trei geodezii poate fi extinsă la poliedre convexe, luând în considerare cvasigeodezice, curbe care sunt geodezice, cu excepția vârfurilor poliedrelor și care au unghiuri mai mici de π pe ambele părți la fiecare vârf pe care îl traversează. O versiune a teoremei celor trei geodezice pentru poliedre convexe afirmă că toate poliedrele au cel puțin trei cvasigeodezice închise simple; acest lucru poate fi dovedit prin aproximarea poliedrului de o suprafață netedă și aplicarea teoremei celor trei geodezii pe această suprafață. Este o problemă deschisă dacă oricare dintre aceste cvasigeodezice poate fi construită în timp polinomial .