Clasificarea discontinuităților - Classification of discontinuities

Funcțiile continue sunt de cea mai mare importanță în matematică , funcții și aplicații. Cu toate acestea, nu toate funcțiile sunt continue . Dacă o funcție nu este continuă într-un punct din domeniul său , se spune că are o discontinuitate acolo. Setul tuturor punctelor de discontinuitate a unei funcții poate fi un set discret , un set de dens , sau chiar întregul domeniu al funcției. Acest articol descrie clasificarea discontinuități în cel mai simplu caz de funcții ale unui singur reală variabilă cu valori reale.

Oscilație a unei funcții într - un punct cuantifică aceste discontinuități , după cum urmează:

• într-o discontinuitate detașabilă , distanța cu care valoarea funcției este dezactivată este oscilația ;
• într-o discontinuitate a săriturii , mărimea saltului este oscilația (presupunând că valoarea la punctul se află între aceste limite ale celor două părți);
• într - o esențială discontinuitate , oscilație măsoară eșecul unei limite de a exista ; limita este constantă.

Un caz special este dacă funcția divergă la infinit sau minus infinit , caz în care oscilația nu este definită (în numerele reale extinse, aceasta este o discontinuitate amovibilă).

Clasificare

Pentru fiecare dintre următoarele, considerați o funcție reală f a unei variabile reale x , definită într-o vecinătate a punctului x ₀ la care f este discontinuu.

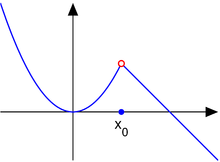
Discontinuitate detașabilă

Luați în considerare funcția în bucăți

${\ displaystyle f (x) = {\ begin {cases} x ^ {2} & {\ mbox {for}} x <1 \\ 0 & {\ mbox {for}} x = 1 \\ 2-x & {\ mbox {for}} x> 1 \ end {cases}}}$

Punctul x ₀ = 1 este o discontinuitate amovibilă . Pentru acest tip de discontinuitate:

Limita-o singură față de direcția negativă:

${\ displaystyle L ^ {-} = \ lim _ {x \ to x_ {0} ^ {-}} f (x)}$

și limita unilaterală din direcția pozitivă:

${\ displaystyle L ^ {+} = \ lim _ {x \ to x_ {0} ^ {+}} f (x)}$

la x ₀ ambele există, sunt finite și sunt egale cu L = L ^- = L ⁺ . Cu alte cuvinte, deoarece cele două limite unilaterale există și sunt egale, limita L a f ( x ) pe măsură ce x se apropie de x ₀ există și este egală cu aceeași valoare. Dacă valoarea reală a lui f ( x ₀ ) nu este egală cu L , atunci x ₀ se numește discontinuitate amovibilă . Această discontinuitate poate fi eliminată pentru a face f continuă la x ₀ , sau mai precis, funcția

${\ displaystyle g (x) = {\ begin {cases} f (x) & x \ neq x_ {0} \\ L & x = x_ {0} \ end {cases}}}$

este continuu la x = x ₀ .

Termenul de discontinuitate amovibil este uneori extins pentru a include o singularitate amovibilă , în care limitele în ambele direcții există și sunt egale, în timp ce funcția este nedefinită la punctul x ₀ . Această utilizare este un abuz de terminologie deoarece continuitatea și discontinuitatea unei funcții sunt concepte definite numai pentru puncte din domeniul funcției.

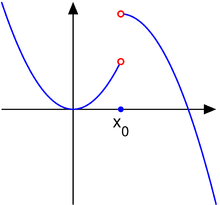
Salt discontinuitatea

Luați în considerare funcția

${\ displaystyle f (x) = {\ begin {cases} x ^ {2} & {\ mbox {for}} x <1 \\ 0 & {\ mbox {for}} x = 1 \\ 2- (x- 1) ^ {2} & {\ mbox {for}} x> 1 \ end {cases}}}$

Apoi, punctul x ₀ = 1 este o discontinuitate de salt .

În acest caz, o singură limită nu există deoarece limitele unilaterale, L ^- și L ⁺ , există și sunt finite, dar nu sunt egale: deoarece, L ^- ≠ L ⁺ , limita L nu există. Apoi, x ₀ se numește discontinuitate de salt , discontinuitate în trepte sau discontinuitate de primul fel . Pentru acest tip de discontinuitate, funcția f poate avea orice valoare la x ₀ .

Discontinuitate esențială

Pentru o discontinuitate esențială, cel puțin una dintre cele două limite unilaterale nu există. Luați în considerare funcția

${\ displaystyle f (x) = {\ begin {cases} \ sin {\ frac {5} {x-1}} și {\ text {for}} x <1 \\ 0 & {\ text {for}} x = 1 \\ {\ frac {1} {x-1}} și {\ text {for}} x> 1. \ end {cases}}}$

Apoi, punctul este o discontinuitate esențială . ${\ displaystyle x_ {0} = 1}$

În acest exemplu, ambele și nu există, satisfăcând astfel condiția discontinuității esențiale. Deci x ₀ este o discontinuitate esențială, discontinuitate infinită sau discontinuitate de al doilea fel. (Acest lucru este distinct de o singularitate esențială , care este adesea utilizată atunci când studiază funcțiile variabilelor complexe .) ${\ displaystyle L ^ {-}}$${\ displaystyle L ^ {+}}$

Ansamblul discontinuităților unei funcții

Să presupunem că f este o funcție definită pe un interval . Vom nota prin setul tuturor discontinuităților de pe intervalul funcției f . Următoarele două proprietăți ale setului sunt relevante în literatura de specialitate. ${\ displaystyle I \ subset \ mathbb {R}}$${\ displaystyle D}$${\ displaystyle I}$${\ displaystyle D}$

• Mulțimea lui este o mulțime F _σ . Setul de puncte la care o funcție este continuă este întotdeauna un set G _δ .${\ displaystyle D}$

• Dacă pe intervalul , f este monoton , atunci este cel mult numărabilă . Aceasta este teorema lui Froda .${\ displaystyle I}$${\ displaystyle D}$
• Când și f este o funcție mărginită, este bine cunoscută importanța setului în ceea ce privește integrabilitatea Riemann a lui f . De fapt, teorema Lebesgue-Vitali afirmă că f este Riemann integrabil dacă și numai dacă are măsura lui Lebesgue nulă.${\ displaystyle I = [a, b]}$${\ displaystyle D}$${\ displaystyle I = [a, b]}$${\ displaystyle D}$

Pentru Lebesgue-Vitali se pare că toate tipurile de discontinuități au aceeași greutate asupra obstrucției pe care o funcție mărginită f poate fi integrată Riemann . Cu toate acestea, nu este cazul. De fapt, anumite discontinuități nu au absolut niciun rol asupra integrabilității Riemann a funcției. Pentru a clarifica această întrebare, merită să împărțiți setul în următoarele trei seturi corespunzătoare tipului de discontinuități avute în vedere inițial. ${\ displaystyle [a, b]}$${\ displaystyle D}$

În acest scop, vom înțelege ansamblul tuturor, astfel încât f are o discontinuitate detașabilă la . În mod analog prin denotăm mulțimea constituită din toate astfel încât f are o discontinuitate de salt la . Mulțimea tuturor celor care f are o discontinuitate esențială la va fi notată cu . Desigur, ansamblul tuturor discontinuităților pe intervalul funcției f este astfel încât . ${\ displaystyle R}$${\ displaystyle x_ {0} \ în I}$${\ displaystyle x_ {0}}$${\ displaystyle J}$${\ displaystyle x_ {0} \ în I}$${\ displaystyle x_ {0}}$${\ displaystyle x_ {0} \ în I}$${\ displaystyle x_ {0}}$${\ displaystyle E}$${\ displaystyle D}$${\ displaystyle I}$${\ displaystyle D = R \ cup J \ cup E}$

Setul tuturor discontinuităților esențiale poate fi împărțit în următoarele două seturi: ${\ displaystyle E}$

${\ displaystyle E_ {1} = \ {x_ {0} \ în E: \ lim _ {x \ to x_ {0} ^ {-}} f (x)}$și nu există și nici sau exit . ${\ displaystyle \ lim _ {x \ to x_ {0} ^ {+}} f (x)}$${\ displaystyle \}}$${\ displaystyle E_ {2} = \ {x_ {0} \ în E:}$${\ displaystyle \ lim _ {x \ to x_ {0} ^ {-}} f (x)}$${\ displaystyle \ lim _ {x \ to x_ {0} ^ {+}} f (x)}$${\ displaystyle \}}$

Desigur . Ori de câte ori vom spune că este o discontinuitate esențială de primă natură . Pentru orice o vom numi o discontinuitate esențială de al doilea fel.${\ displaystyle E = E_ {1} \ cup E_ {2}}$${\ displaystyle x_ {0} \ în E_ {1}}$${\ displaystyle x_ {0}}$${\ displaystyle x_ {0} \ în E_ {2}}$

Una are următoarea proprietate importantă (a se vedea):

• Setul este numărabil.${\ displaystyle R \ cup J \ cup E_ {2}}$

Prin urmare, teorema Lebesgue-Vitali poate fi reformulată după cum urmează:

• O funcție mărginită, f , este Riemann integrabilă dacă și numai dacă setul corespondent al tuturor discontinuităților esențiale ale primului tip de f are măsura lui Lebesgue nulă.${\ displaystyle [a, b]}$${\ displaystyle E_ {1}}$

Funcția lui Thomae este discontinuă la fiecare punct rațional non-zero , dar continuă la fiecare punct irațional . Se vede cu ușurință că aceste discontinuități sunt toate esențiale de prima natură. În primul paragraf, nu există o funcție continuă în fiecare punct rațional , dar discontinuă în fiecare punct irațional.

Funcția indicator a raționalelor, cunoscută și sub numele de funcția Dirichlet , este discontinuă peste tot . Aceste discontinuități sunt toate esențiale și de prima natură.

Exemplu

Luați în considerare acum setul Cantor și funcția sa de indicator (sau caracteristică)${\ displaystyle {\ mathcal {C}} \ subset [0,1]}$

Având în vedere discontinuitățile acestei funcții, să presupunem un punct . Prin urmare, există un set , utilizat în formularea lui , care nu conține . Adică aparține unuia dintre intervalele deschise care au fost eliminate în construcția . În acest fel, există un vecinătate fără puncte de , unde, în consecință, își asumă doar valoarea zero. Prin urmare este continuu în . Aceasta înseamnă că setul tuturor discontinuităților de pe interval este un subset de . Deoarece este un set necontabil cu măsură Lebesgue nulă, este și un set nul de măsuri Lebesgue și deci, în ceea ce privește teorema Lebesgue-Vitali, este o funcție integrabilă Riemann. ${\ displaystyle x_ {0} \ not \ in {\ mathcal {C}}}$${\ displaystyle C_ {n}}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle x_ {0}}$${\ displaystyle x_ {0}}$${\ displaystyle C_ {n}}$${\ displaystyle x_ {0}}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle \ mathbf {1} _ {\ mathcal {C}} (x)}$${\ displaystyle \ mathbf {1} _ {\ mathcal {C}}}$${\ displaystyle x_ {0}}$${\ displaystyle D}$${\ displaystyle \ mathbf {1} _ {\ mathcal {C}}}$${\ displaystyle [0,1]}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle D}$${\ displaystyle \ mathbf {1} _ {\ mathcal {C}}}$

Dar mai exact unul are . De fapt, dacă nu poate fi cuprins niciun vecin din . În caz contrar , ar trebui să avem, pentru fiecare , , ceea ce este absurd. întrucât fiecare dintre aceste seturi este compus din interval cu lungime , ceea ce nu permite includerea respectivă pentru valori suficient de mari în așa fel încât . În acest fel, orice vecinătate de conține puncte și puncte care nu sunt . În ceea ce privește funcția, aceasta înseamnă că ambele și nu există. Adică , unde , ca și mai înainte, denotăm setul tuturor discontinuităților esențiale ale primului tip de funcție . Clar${\ displaystyle D = {\ mathcal {C}}}$${\ displaystyle x_ {0} \ in {\ mathcal {C}}}$${\ displaystyle {\ bigl (} x_ {0} - \ epsilon, x_ {0} + \ epsilon {\ bigr)}}$${\ displaystyle x_ {0}}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle n}$${\ displaystyle {\ bigl (} x_ {0} - \ epsilon, x_ {0} + \ epsilon {\ bigr)} \ subset C_ {n}}$${\ displaystyle 3 ^ {- n}}$${\ displaystyle n}$${\ displaystyle 3 ^ {- n} <\ epsilon}$${\ displaystyle x_ {0} \ in {\ mathcal {C}}}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle \ mathbf {1} _ {\ mathcal {C}}}$${\ displaystyle \ lim _ {x \ to x_ {0} ^ {-}} \ mathbf {1} _ {\ mathcal {C}} (x)}$${\ displaystyle \ lim _ {x \ to x_ {0} ^ {+}} 1 _ {\ mathcal {C}} (x)}$${\ displaystyle D = E_ {1}}$${\ displaystyle E_ {1}}$${\ displaystyle \ mathbf {1} _ {\ mathcal {C}}}$${\ displaystyle \ int _ {0} ^ {1} \ mathbf {1} _ {\ mathcal {C}} (x) dx = 0.}$

Vezi si

• Singularitate detașabilă
• Singularitate matematică
• Extindere prin continuitate
• Finete
  • Continuitate geometrică
  • Continuitate parametrică

Note

Referințe

Surse

• Malik, SC; Arora, Savita (1992). Analiza matematică (ediția a II-a). New York: Wiley. ISBN 0-470-21858-4.

linkuri externe

• „Discontinuu” . PlanetMath .
• „Discontinuitatea” de Ed Pegg, Jr. , The Wolfram Demonstrations Project , 2007.
• Weisstein, Eric W. „Discontinuitate” . MathWorld .
• Kudryavtsev, LD (2001) [1994], „Discontinuity point” , Enciclopedia Matematicii , EMS Press