Criteriul Kelly - Kelly criterion

În teoria probabilității , criteriul Kelly (sau strategia Kelly sau pariul Kelly ), este o formulă care determină dimensiunea teoretică optimă pentru un pariu. Este valabil atunci când sunt cunoscute randamentele așteptate. Mărimea pariului Kelly se găsește prin maximizarea valorii așteptate a logaritmului bogăției, care este echivalentă cu maximizarea ratei de creștere geometrică așteptată. A fost descris de JL Kelly Jr , cercetător la Bell Labs , în 1956. Criteriul este cunoscut și ca metoda științifică a jocurilor de noroc, deoarece conduce la o bogăție mai mare comparativ cu orice altă strategie pe termen lung (adică rentabilitatea maximă teoretică ca numărul de pariuri merge la infinit).

Utilizarea practică a formulei a fost demonstrată pentru jocurile de noroc și aceeași idee a fost folosită pentru a explica diversificarea în gestionarea investițiilor . În anii 2000, analiza în stil Kelly a devenit o parte a teoriei investițiilor principale și s-a susținut că investitorii de succes cunoscuți, inclusiv Warren Buffett și Bill Gross, folosesc metode Kelly. William Poundstone a scris o relatare populară extinsă despre istoria pariurilor Kelly. A se vedea, de asemenea , alegerea portofoliului Intertemporal .

Exemplu optim de pariere

Utilitatea sumei de pariere Kelly poate fi realizată comparând-o cu alte strategii de jocuri de noroc.

Într-un studiu, fiecărui participant i s-au acordat 25 de dolari și i s-a cerut să plaseze pariuri pe bani echitabili pe o monedă care ar obține capete 60% din timp. Participanții au avut 30 de minute pentru a juca, așa că ar putea plasa aproximativ 300 de pariuri, iar premiile au fost limitate la 250 USD. Pariul Kelly în acest scenariu este de 20%, ceea ce rezultă la un câștig mediu de 2% în fiecare rundă. Câștigurile medii așteptate cu 300 de runde se ridică la 10.500 USD dacă nu ar fi plafonat. Dar comportamentul subiecților testului a fost departe de a fi optim:

În mod remarcabil, 28% dintre participanți au dat faliment, iar plata medie a fost de doar 91 USD. Doar 21% dintre participanți au atins maximul. 18 din cei 61 de participanți au pariat totul într-o singură aruncare, în timp ce două treimi au jucat la coadă la un moment dat al experimentului.

Dacă pariorii ar fi urmat pariul Kelly, este de așteptat ca 94% dintre participanți să fi ajuns la limita maximă.

Formula de jocuri de noroc

În cazul în care pierderea pariului implică pierderea întregului pariu, pariul Kelly este:

${\ displaystyle f ^ {*} = p - {\ frac {q} {b}} = p + {\ frac {p-1} {b}}}$

Unde:

• ${\ displaystyle f ^ {*}}$ este fracția din pariul curent de pariat.
• ${\ displaystyle p}$ este probabilitatea unei victorii.
• ${\ displaystyle q}$este probabilitatea unei pierderi ( ).${\ displaystyle q = 1-p}$
• ${\ displaystyle b}$este suma câștigată cu o victorie. De exemplu, dacă pariați 10 USD pe un pariu de cote 2 la 1 , (la câștig vi se returnează 30 USD, câștigând 20 USD), atunci .${\ displaystyle b = \ 20 $ / \ 10 $ = 2.0}$

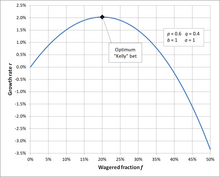
De exemplu, dacă un pariu are șanse de 60% de câștig ( , ), iar jucătorul primește cote 1 la 1 pe un pariu câștigător ( ), atunci jucătorul ar trebui să parieze 20% din bankroll la fiecare oportunitate ( ) , pentru a maximiza rata de creștere pe termen lung a bankroll-ului. ${\ displaystyle p = 0.6}$${\ displaystyle q = 0.4}$${\ displaystyle b = 1}$${\ displaystyle f ^ {*} = 0.6 - {\ frac {0.4} {1}} = 0.2}$

Dacă jucătorul are margine zero, adică dacă , atunci criteriul recomandă jucătorului să nu parieze nimic. ${\ displaystyle b = q / p}$

Dacă marginea este negativă ( ) formula dă un rezultat negativ, indicând faptul că jucătorul ar trebui să ia cealaltă parte a pariului. De exemplu, în ruleta americană , pariorului i se oferă o plată de bani uniformă ( ) pe roșu, atunci când pe roată sunt 18 numere roșii și 20 de numere non-roșii ( ). Pariul Kelly este , adică jucătorul ar trebui să parieze un al nouăsprezecelea din bancroll, că roșul nu va apărea. Nu există niciun pariu explicit anti-roșu oferit cu cote comparabile în ruletă, așa că cel mai bun lucru pe care îl poate face un jucător Kelly este să nu pariezi nimic. ${\ displaystyle b <q / p}$${\ displaystyle b = 1}$${\ displaystyle p = 18/38}$${\ displaystyle -1/19}$

Formula de investiții

O formă mai generală a formulei Kelly permite pierderi parțiale, care sunt relevante pentru investiții:

${\ displaystyle f ^ {*} = {\ frac {p} {a}} - {\ frac {q} {b}}.}$

Unde:

• ${\ displaystyle f ^ {*}}$ este fracțiunea activelor care se aplică garanției.
• ${\ displaystyle p}$ este probabilitatea ca investiția să crească în valoare.
• ${\ displaystyle q}$este probabilitatea ca investiția să scadă în valoare ( ).${\ displaystyle q = 1-p}$
• ${\ displaystyle a}$este fracția care se pierde într-un rezultat negativ. De exemplu, dacă prețul securității scade cu 10%, atunci${\ displaystyle a = 0.1}$
• ${\ displaystyle b}$este fracția care se câștigă într-un rezultat pozitiv. De exemplu, dacă prețul securității crește cu 10%, atunci .${\ displaystyle b = 0.1}$

Rețineți că criteriul Kelly este valabil numai pentru probabilitățile de rezultate cunoscute , ceea ce nu este cazul investițiilor. Nu este recomandată investiția întregii fracțiuni Kelly.

Această formulă poate avea ca rezultat fracțiuni Kelly mai mari de 1. În acest caz, este teoretic avantajos să utilizați efectul de levier pentru a cumpăra titluri suplimentare pe marjă .

Dovadă

Dovezile euristice ale criteriului Kelly sunt simple. Criteriul Kelly maximizează valoarea așteptată a logaritmului bogăției (valoarea așteptării unei funcții este dată de suma, peste toate rezultatele posibile, a probabilității fiecărui rezultat particular înmulțit cu valoarea funcției în cazul acelui rezultat ). Începem cu o unitate de avere și pariez o fracțiune din acea avere pe un rezultat care apare cu probabilitate și oferă cote de . Probabilitatea de a câștiga este și, în acest caz, bogăția rezultată este egală cu . Probabilitatea de a pierde este și, în acest caz, bogăția rezultată este egală cu . Prin urmare, rata de creștere geometrică așteptată este: ${\ displaystyle f}$${\ displaystyle p}$${\ displaystyle b}$${\ displaystyle p}$${\ displaystyle 1 + fb}$${\ displaystyle q = 1-p}$${\ displaystyle 1-fa}$${\ displaystyle r}$

${\ displaystyle r = (1 + fb) ^ {p} \ cdot (1-fa) ^ {q}}$

Vrem să găsim rul maxim al acestei curbe, care implică găsirea derivatei ecuației. Acest lucru se realizează mai ușor luând mai întâi logaritmul fiecărei părți. Ecuația rezultată este:

${\ displaystyle E = \ log (r) = p \ log (1 + fb) + q \ log (1-fa)}$

cu denotarea creșterii bogăției logaritmice. Pentru a găsi valoarea pentru care rata de creștere este maximizată, notată ca , diferențiem expresia de mai sus și o setăm egală cu zero. Asta da: ${\ displaystyle E}$${\ displaystyle f}$${\ displaystyle f ^ {*}}$

${\ displaystyle \ left. {\ frac {dE} {df}} \ right | _ {f = f ^ {*}} = {\ frac {pb} {1 + f ^ {*} b}} + {\ frac {-qa} {1-f ^ {*} a}} = 0}$

Rearanjarea acestei ecuații pentru a rezolva valoarea lui oferă criteriul Kelly: ${\ displaystyle f ^ {*}}$

${\ displaystyle f ^ {*} = {\ frac {p} {a}} - {\ frac {q} {b}}}$

Observați că această expresie se reduce la formula simplă de jocuri de noroc atunci când , atunci când o pierdere are ca rezultat pierderea completă a pariului. ${\ displaystyle a = 1 = 100 \%}$

Bernoulli

Într-un articol din 1738, Daniel Bernoulli a sugerat că, atunci când cineva poate alege pariuri sau investiții, ar trebui să o aleagă pe cea cu cea mai mare medie geometrică de rezultate. Acest lucru este echivalent matematic cu criteriul Kelly, deși motivația este complet diferită (Bernoulli a dorit să rezolve paradoxul de la Sankt Petersburg ).

O traducere în limba engleză a articolului Bernoulli nu a fost publicată până în 1954, dar lucrarea a fost bine cunoscută printre matematicieni și economiști.

Aplicarea la bursa

În finanțele matematice, un portofoliu se numește creștere optimă dacă ponderile de securitate maximizează rata de creștere geometrică așteptată (care este echivalentă cu maximizarea bogăției logare).

Calculele portofoliilor optime de creștere pot suferi probleme uriașe de gunoi, de gunoi. De exemplu, cazurile de mai jos iau în considerare rentabilitatea așteptată și structura de covarianță a diferitelor active, dar acești parametri sunt cel mai bine estimate sau modelate cu o incertitudine semnificativă. Performanța ex-post a unui portofoliu de creștere optim poate diferi în mod fantastic cu predicția ex-ante dacă ponderile portofoliului sunt în mare parte determinate de erori de estimare. Abordarea incertitudinii parametrilor și a erorii de estimare este un subiect important în teoria portofoliului. O abordare pentru a contracara riscul necunoscut este de a investi mai puțin decât criteriul Kelly, de exemplu jumătate.

Critică

Deși promisiunea strategiei Kelly de a face mai bine decât orice altă strategie pe termen lung pare convingătoare, unii economiști s-au argumentat puternic împotriva acesteia, în principal pentru că constrângerile specifice de investiție ale unui individ pot depăși dorința unei rate de creștere optime. Alternativa convențională este de așteptat de utilitate teorie care spune ca pariurile să fie dimensionate pentru a maximiza de așteptat , utilitatea rezultatului (la un individ cu logaritmică utilitate, pariul Kelly maximizează utilitatea de așteptat, astfel încât nu există nici un conflict, în plus, hârtia originală Kelly afirmă în mod clar necesitatea unei funcții utilitare în cazul jocurilor de noroc care se joacă finit de multe ori). Chiar și susținătorii Kelly susțin de obicei Kelly fracționată (parierea unei fracții fixe din suma recomandată de Kelly) din mai multe motive practice, cum ar fi dorința de a reduce volatilitatea sau protejarea împotriva erorilor nedeterministe în calculele lor de avantaj (margine).

Matematică avansată

Pentru o dovadă riguroasă și generală, consultați lucrarea originală a lui Kelly sau câteva dintre celelalte referințe enumerate mai jos. Au fost publicate unele corecții. Oferim următorul argument neriguros pentru cazul cu (un pariu de 50:50 „chiar bani”) pentru a arăta ideea generală și a oferi câteva informații. Când , un parior Kelly pariază de bogăția inițială , așa cum se arată mai sus. Dacă câștigă, au după un pariu. Dacă pierd, au . Să presupunem că fac pariuri de acest fel și câștigă ori din această serie de pariuri. Bogăția rezultată va fi: ${\ displaystyle b = 1}$${\ displaystyle b = 1}$${\ displaystyle 2p-1}$${\ displaystyle W}$${\ displaystyle 2pW}$${\ displaystyle 2 (1-p) W}$${\ displaystyle N}$${\ displaystyle K}$${\ displaystyle N}$

${\ displaystyle 2 ^ {N} p ^ {K} (1-p) ^ {NK} W \ !.}$

Rețineți că ordonarea câștigurilor și pierderilor nu afectează bogăția rezultată. Să presupunem că un alt parior pariază o sumă diferită, pentru o anumită valoare de (unde poate fi pozitiv sau negativ). Vor avea după o victorie și după o pierdere. După aceeași serie de victorii și pierderi ca pariorul Kelly, vor avea: ${\ displaystyle (2p-1 + \ Delta) W}$${\ displaystyle \ Delta}$${\ displaystyle \ Delta}$${\ displaystyle (2p + \ Delta) W}$${\ displaystyle [2 (1-p) - \ Delta] W}$

${\ displaystyle (2p + \ Delta) ^ {K} [2 (1-p) - \ Delta] ^ {NK} W}$

Luați derivatul acestui lucru și obțineți: ${\ displaystyle \ Delta}$

${\ displaystyle K (2p + \ Delta) ^ {K-1} [2 (1-p) - \ Delta] ^ {NK} W- (NK) (2p + \ Delta) ^ {K} [2 (1-p ) - \ Delta] ^ {NK-1} W}$

Funcția este maximizată atunci când această derivată este egală cu zero, care apare la:

${\ displaystyle K [2 (1-p) - \ Delta] = (NK) (2p + \ Delta)}$

ceea ce implică asta

${\ displaystyle \ Delta = 2 \ left ({\ frac {K} {N}} - p \ right)}$

dar proporția de pariuri câștigătoare va converge în cele din urmă către:

${\ displaystyle \ lim _ {N \ to + \ infty} {\ frac {K} {N}} = p}$

conform legii slabe a numărului mare . Deci, pe termen lung, bogăția finală este maximizată prin setarea la zero, ceea ce înseamnă urmarea strategiei Kelly. Acest lucru ilustrează faptul că Kelly are atât o componentă deterministă, cât și o componentă stocastică. Dacă se cunoaște K și N și dorește să aleagă o fracție constantă de avere pentru a paria de fiecare dată (altfel s-ar putea înșela și, de exemplu, paria zero după K ^a câștigat știind că restul pariurilor vor pierde), se va termina cu cei mai mulți bani dacă pariați: ${\ displaystyle \ Delta}$

${\ displaystyle \ left (2 {\ frac {K} {N}} - 1 \ right) W}$

de fiecare data. Acest lucru este adevărat, indiferent dacă este mic sau mare. Partea „pe termen lung” a lui Kelly este necesară deoarece K nu este cunoscută în prealabil, doar că, pe măsură ce devine mare, se va apropia . Cineva care pariază mai mult decât Kelly se poate descurca mai bine dacă este pentru o perioadă; cineva care pariază mai puțin decât Kelly poate face mai bine dacă pentru o perioadă, dar pe termen lung, Kelly câștigă întotdeauna. Dovada euristică pentru cazul general se desfășoară după cum urmează. Într-un singur studiu, dacă investiți fracțiunea de capital, dacă strategia dvs. reușește, capitalul dvs. la sfârșitul procesului crește cu factorul și, la fel, dacă strategia eșuează, ajungeți să vă scădeați capitalul cu factor . Astfel, la sfârșitul încercărilor (cu succese și eșecuri), capitalul inițial de 1 $ cedează ${\ displaystyle N}$${\ displaystyle N}$${\ displaystyle K}$${\ displaystyle pN}$${\ displaystyle K> pN}$${\ displaystyle K <pN}$${\ displaystyle f}$${\ displaystyle 1-f + f (1 + b) = 1 + fb}$${\ displaystyle 1-fa}$${\ displaystyle N}$${\ displaystyle pN}$${\ displaystyle qN}$

${\ displaystyle C_ {N} = (1 + fb) ^ {pN} (1-fa) ^ {qN}.}$

Maximizarea și, în consecință , în ceea ce privește conduce la rezultatul dorit ${\ displaystyle \ log (C_ {N}) / N}$${\ displaystyle C_ {N}}$${\ displaystyle f}$

${\ displaystyle f ^ {*} = p / aq / b.}$

Edward O. Thorp a oferit o discuție mai detaliată a acestei formule pentru cazul general. Acolo, se poate observa că înlocuirea raportului dintre numărul de "succese" și numărul de studii implică faptul că numărul de studii trebuie să fie foarte mare, deoarece este definit ca limita acestui raport ca numărul de studii merge la infinit. Pe scurt, pariurile de fiecare dată vor maximiza probabil rata de creștere a bogăției numai în cazul în care numărul de probe este foarte mare și sunt aceleași pentru fiecare proces. În practică, aceasta este o chestiune de a juca același joc iar și iar, unde probabilitatea de a câștiga și cotele de plată sunt întotdeauna aceleași. În dovada euristică de mai sus, succesele și eșecurile sunt foarte probabil doar pentru foarte mari . ${\ displaystyle p}$${\ displaystyle p}$${\ displaystyle f ^ {*}}$${\ displaystyle p}$${\ displaystyle b}$${\ displaystyle pN}$${\ displaystyle qN}$${\ displaystyle N}$

Rezultate multiple

Criteriul lui Kelly poate fi generalizat pe jocurile de noroc pe multe rezultate care se exclud reciproc, cum ar fi în cursele de cai. Să presupunem că există mai multe rezultate care se exclud reciproc. Probabilitatea ca cel de - al cincilea cal să câștige cursa este , cantitatea totală de pariuri plasate pe -al calul este și ${\ displaystyle k}$${\ displaystyle p_ {k}}$${\ displaystyle k}$${\ displaystyle B_ {k}}$

${\ displaystyle \ beta _ {k} = {\ frac {B_ {k}} {\ sum _ {i} B_ {i}}} = {\ frac {D} {1 + Q_ {k}}},}$

unde sunt cotele de plată. , este rata dividendului în care este preluarea pistei sau impozitul, este rata veniturilor după deducerea prelevării pistei când câștigă al treilea cal. Fracția din fondurile pariorului pentru a paria pe calul al doilea este . Criteriul lui Kelly pentru jocurile de noroc cu multiple rezultate care se exclud reciproc oferă un algoritm pentru găsirea setului optim de rezultate pe care este rezonabil să pariezi și oferă o formulă explicită pentru găsirea fracțiilor optime din averea pariorului care să fie pariat pe rezultatele incluse în setul optim . Algoritmul pentru setul optim de rezultate constă din patru pași. ${\ displaystyle Q_ {k}}$${\ displaystyle D = 1-tt}$${\ displaystyle tt}$${\ displaystyle {\ frac {D} {\ beta _ {k}}}}$${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle f_ {k}}$${\ displaystyle S ^ {o}}$${\ displaystyle f_ {k} ^ {o}}$${\ displaystyle S ^ {o}}$

Pasul 1 : Calculați rata de venituri așteptată pentru toate rezultatele posibile (sau numai pentru mai multe dintre cele mai promițătoare) rezultate:

${\ displaystyle er_ {i} = {\ frac {Dp_ {i}} {\ beta _ {i}}} = p_ {i} (Q_ {i} +1)}$

Pasul 2 : Reordonați rezultatele astfel încât noua secvență să nu crească. Astfel va fi cel mai bun pariu.${\ displaystyle er_ {k}}$${\ displaystyle er_ {1}}$

Pasul 3 : Set (setul gol) ,, . Astfel cel mai bun pariu va fi considerat primul.${\ displaystyle S = \ varnothing}$${\ displaystyle k = 1}$${\ displaystyle R (S) = 1}$${\ displaystyle er_ {k} = er_ {1}}$

Pasul 4 : Repetați:

Dacă apoi introduceți al treilea rezultat în set :, recalculați conform formulei: ${\ displaystyle er_ {k} = {\ frac {D} {\ beta _ {k}}} p_ {k}> R (S)}$${\ displaystyle k}$${\ displaystyle S = S \ cup \ {k \}}$${\ displaystyle R (S)}$

${\ displaystyle R (S) = {\ frac {D \ sum _ {k \ notin S} p_ {k}} {D- \ sum _ {k \ in S} \ beta _ {k}}}}$ și apoi set ,${\ displaystyle k = k + 1}$

În caz contrar, setați și opriți repetarea.${\ displaystyle S ^ {o} = S}$

Dacă setul optim este gol, atunci nu pariați deloc. Dacă setul de rezultate optime nu este gol, atunci fracțiunea optimă pentru a paria pe rezultatul al cincilea poate fi calculată din această formulă: ${\ displaystyle S ^ {o}}$${\ displaystyle S ^ {o}}$${\ displaystyle f_ {k} ^ {o}}$${\ displaystyle k}$

${\ displaystyle f_ {i} = p_ {i} - \ beta _ {i} {\ frac {\ sum _ {k \ notin S} p_ {k}} {(D- \ sum _ {k \ in S} \ beta _ {k})}}}$.

Se poate dovedi asta

${\ displaystyle R (S ^ {o}) = 1- \ sum _ {i \ in S ^ {o}} {f_ {i} ^ {o}}}$

unde partea dreaptă este rata de rezervă. Prin urmare, cerința poate fi interpretată după cum urmează: - al treilea rezultat este inclus în setul de rezultate optime dacă și numai dacă rata de venituri așteptată este mai mare decât rata de rezervă. Formula pentru fracția optimă poate fi interpretată ca excesul ratei veniturilor așteptat de cal peste rata -lea rezervelor împărțită la venitul după deducerea preluării pista atunci când câștigă cal sau ca -lea excesul de probabilitatea -lea calul câștigă rata de rezervă împărțită la venituri după deducerea pistei luate atunci când al cincilea cal câștigă. Exponentul de creștere binar este ${\ displaystyle er_ {k} = {\ frac {D} {\ beta _ {k}}} p_ {k}> R (S)}$${\ displaystyle k}$${\ displaystyle S ^ {o}}$${\ displaystyle f_ {k} ^ {o}}$${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle k}$

${\ displaystyle G ^ {o} = \ sum _ {i \ in S} {p_ {i} \ log _ {2} {(er_ {i})}} + (1- \ sum _ {i \ in S } {p_ {i}}) \ log _ {2} {(R (S ^ {o}))}}$

iar timpul de dublare este

${\ displaystyle T_ {d} = {\ frac {1} {G ^ {o}}}.}$

Această metodă de selecție a pariurilor optime poate fi aplicată și atunci când probabilitățile sunt cunoscute numai pentru câteva rezultate dintre cele mai promițătoare, în timp ce rezultatele rămase nu au nicio șansă de a câștiga. În acest caz trebuie să fie că ${\ displaystyle p_ {k}}$

${\ displaystyle \ sum _ {i} {p_ {i}} <1,}$ și

${\ displaystyle \ sum _ {i} {\ beta _ {i}} <1}$.

Investiții pe acțiuni

Polinomul Taylor de ordinul doi poate fi folosit ca o bună aproximare a criteriului principal. În primul rând, este util pentru investițiile în acțiuni, unde fracția dedicată investiției se bazează pe caracteristici simple care pot fi ușor estimate din datele istorice existente - valoarea și varianța așteptate . Această aproximare duce la rezultate robuste și care oferă rezultate similare cu criteriul inițial.

Pentru active unice (acțiuni, fonduri indexate etc.) și o rată fără riscuri, este ușor să obțineți fracțiunea optimă pentru a investi prin mișcare browniană geometrică . Valoarea unui material distribuit lognormal la momentul ( ) este ${\ displaystyle S}$${\ displaystyle t}$${\ displaystyle S_ {t}}$

${\ displaystyle S_ {t} = S_ {0} \ exp \ left (\ left (\ mu - {\ frac {\ sigma ^ {2}} {2}} \ right) t + \ sigma W_ {t} \ right ),}$

din soluția mișcării browniene geometrice unde este un proces Wiener și (deriva procentuală) și (volatilitatea procentuală) sunt constante. Așteptările logaritmului: ${\ displaystyle W_ {t}}$${\ displaystyle \ mu}$${\ displaystyle \ sigma}$

${\ displaystyle \ mathbb {E} \ log (S_ {t}) = \ log (S_ {0}) + \ left (\ mu - {\ frac {\ sigma ^ {2}} {2}} \ right) t.}$

Apoi, returnarea jurnalului așteptată este ${\ displaystyle R_ {s}}$

${\ displaystyle R_ {s} = \ left (\ mu - {\ frac {\ sigma ^ {2}} {2}} \, \ right) s.}$

Pentru un portofoliu format dintr-un activ și o rată fără risc care plătește o obligațiune , cu o fracție investită în și în obligațiune, randamentul preconizat pe o perioadă este dat de ${\ displaystyle S}$${\ displaystyle r}$${\ displaystyle f}$${\ displaystyle S}$${\ displaystyle (1-f)}$

${\ displaystyle \ mathbb {E} \ left (f \ left [{\ frac {S_ {1}} {S_ {0}}} - 1 \ right] + (1-f) r \ right) = \ mathbb { E} \ left (f \ left [\ exp \ left (\ left (\ mu - {\ frac {\ sigma ^ {2}} {2}} \ right) + \ sigma W_ {1} \ right) -1 \ dreapta] \ dreapta) + (1-f) r}$

cu toate acestea, oamenii par să se ocupe de rentabilitatea așteptată a jurnalului pentru o perioadă, în schimb, în ​​contextul lui Kelly: ${\ displaystyle G (f)}$

${\ displaystyle G (f) = f \ mu - {\ frac {(f \ sigma) ^ {2}} {2}} + ((1-f) \ r).}$

Rezolvând obținem ${\ displaystyle \ max (G (f))}$

${\ displaystyle f ^ {*} = {\ frac {\ mu -r} {\ sigma ^ {2}}}.}$

${\ displaystyle f ^ {*}}$este fracția care maximizează rentabilitatea logaritmică așteptată, și așa este și fracția Kelly. Thorp a ajuns la același rezultat, dar printr-o derivare diferită. Amintiți-vă că este diferit de returnarea jurnalului de active . Confuzia este o greșeală obișnuită făcută de site-uri și articole care vorbesc despre criteriul Kelly. ${\ displaystyle \ mu}$${\ displaystyle R_ {s}}$

Pentru mai multe active, ia în considerare o piață cu stocuri corelate cu randamente stocastice , și o legătură cu întoarcere fără risc . Un investitor plasează o fracțiune din capitalul lor, iar restul este investit în obligațiune. Fără pierderea generalității, presupuneți că capitalul inițial al investitorului este egal cu 1. Conform criteriului Kelly, ar trebui maximizat ${\ displaystyle n}$${\ displaystyle S_ {k}}$${\ displaystyle r_ {k}}$${\ displaystyle k = 1, ..., n,}$${\ displaystyle r}$${\ displaystyle u_ {k}}$${\ displaystyle S_ {k}}$

${\ displaystyle \ mathbb {E} \ left [\ ln \ left ((1 + r) + \ sum \ limits _ {k = 1} ^ {n} u_ {k} (r_ {k} -r) \ right )\dreapta].}$

Extindând acest lucru cu o serie Taylor în jur , obținem ${\ displaystyle {\ vec {u_ {0}}} = (0, \ ldots, 0)}$

${\ displaystyle \ mathbb {E} \ left [\ ln (1 + r) + \ sum \ limits _ {k = 1} ^ {n} {\ frac {u_ {k} (r_ {k} -r)} {1 + r}} - {\ frac {1} {2}} \ sum \ limits _ {k = 1} ^ {n} \ sum \ limits _ {j = 1} ^ {n} u_ {k} u_ {j} {\ frac {(r_ {k} -r) (r_ {j} -r)} {(1 + r) ^ {2}}} \ right].}$

Astfel, reducem problema de optimizare la programare pătratică și soluția fără restricții este

${\ displaystyle {\ vec {u ^ {\ star}}} = (1 + r) ({\ widehat {\ Sigma}}) ^ {- 1} ({\ widehat {\ vec {r}}} - r )}}$

unde și sunt vectorul mijloacelor și matricea momentelor secundare mixte necentrale ale randamentelor în exces. Există, de asemenea, un algoritm numeric pentru strategiile fracționate Kelly și pentru soluția optimă fără pârghie și fără constrângeri de vânzare în lipsă. ${\ displaystyle {\ widehat {\ vec {r}}}}$${\ displaystyle {\ widehat {\ Sigma}}}$

Vezi si

• Risc de ruină
• Jocurile de noroc și teoria informației
• Paradoxul lui Proebsting
• Problema portofoliului lui Merton

Referințe

linkuri externe