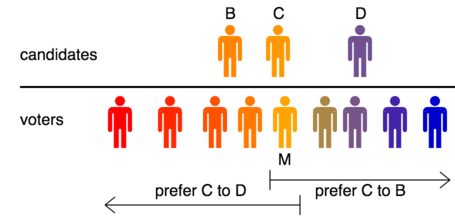
Teorema votantului mediu - Median voter theorem

Alegătorul median teorema este o propunere cu privire la vot preferential pe locul prezentate de Duncan Negre în 1948. Se afirmă că , dacă alegătorii și politicile sunt distribuite de-a lungul unei unidimensional spectru , cu alegătorii alternative de rang în ordinea de proximitate, atunci orice metodă de vot care îndeplinește criteriul Condorcet va alege candidatul cel mai apropiat de alegătorul median. În special, un vot majoritar între două opțiuni va face acest lucru.

Teorema este asociată cu economia alegerii publice și știința politică statistică . Partha Dasgupta și Eric Maskin au susținut că oferă o justificare puternică pentru metodele de vot pe baza criteriului Condorcet. Teorema de echilibru a regulii majorității lui Plott extinde aceasta la două dimensiuni.

O afirmație relativ legată fusese făcută mai devreme (în 1929) de Harold Hotelling . Nu este o adevărată teorema și este cunoscut mai corect ca alegător median teoria sau alegătorului median modelul . Se spune că într-o democrație reprezentativă , politicienii vor converge către punctul de vedere al votantului median.

Enunț și dovadă a teoremei

Candidat C   este cel mai aproape de mediana alegătorului M .

Să presupunem că există un număr impar de alegători și cel puțin doi candidați și să presupunem că opiniile sunt distribuite de-a lungul unui spectru. Să presupunem că fiecare alegător clasează candidații într-o ordine de proximitate astfel încât candidatul cel mai apropiat de alegător să primească prima lor preferință, următorul cel mai apropiat primește a doua preferință și așa mai departe. Apoi, există un votant median și vom arăta că alegerile vor fi câștigate de candidatul care este cel mai apropiat de el.

Dovadă . Votantul mediu să fie Marlene. Candidatul care este cel mai apropiat de ea va primi primul ei vot de preferință. Să presupunem că acest candidat este Charles și că minte în stânga ei. Apoi, Marlene și toți alegătorii din stânga ei (alcătuind o majoritate a electoratului) îl vor prefera pe Charles în fața tuturor candidaților din dreapta sa, iar Marlene și toți alegătorii din dreapta ei îl vor prefera pe Charles în fața tuturor candidaților din stânga sa.

Criteriul Condorcet este definit ca fiind satisfăcut de orice metodă de vot care asigură că un candidat care este preferat oricărui alt candidat de către o majoritate a electoratului va fi câștigătorul, și acesta este exact cazul lui Charles aici; deci rezultă că Charles va câștiga orice alegeri desfășurate folosind o metodă care îndeplinește criteriul Condorcet.

Prin urmare, în orice metodă de vot care îndeplinește criteriul Condorcet, câștigătorul va fi candidatul preferat de votantul median. Pentru deciziile binare , votul majorității îndeplinește criteriul; pentru voturi multi-way, mai multe metode îl satisfac (vezi metoda Condorcet ).

Ipoteze

Teorema se aplică și atunci când numărul alegătorilor este egal, dar detaliile depind de modul de soluționare a legăturilor.

Presupunerea că preferințele sunt exprimate în ordinea proximității poate fi relaxată pentru a spune doar că sunt cu un singur vârf .

Presupunerea că opiniile se află pe o linie reală poate fi relaxată pentru a permite topologii mai generale.

Istorie

Teorema a fost expusă pentru prima dată de Duncan Black în 1948. El a scris că a văzut un decalaj mare în teoria economică referitoare la modul în care votul determină rezultatul deciziilor, inclusiv deciziile politice. Lucrarea lui Black a declanșat cercetări despre modul în care economia poate explica sistemele de vot. În 1957, Anthony Downs a expus teorema electorală mediană în cartea sa „The Economic Theory of Democracy” .

Extindere la distribuții în mai multe dimensiuni

Teorema mediană a alegătorului în două dimensiuni

Teorema mediană a alegătorilor se aplică într-o formă restrânsă la distribuirea opiniilor alegătorilor în spații de orice dimensiune. O distribuție în mai multe dimensiuni nu are neapărat o mediană în toate direcțiile (care ar putea fi denumită „mediană omnidirecțională”); Cu toate acestea o clasă largă de distribuții simetrice rotațional, inclusiv Gaussian , are au o medie de acest tip. Ori de câte ori distribuția alegătorilor are o mediană unică în toate direcțiile și alegătorii clasifică candidații în ordinea apropierii, se aplică teorema alegătorului median: candidatul cel mai apropiat de mediană va avea o preferință majoritară față de toți rivalii și va fi ales de orice metoda de vot care îndeplinește criteriul Condorcet. (Unicitatea generalizează aici proprietatea garantată de ciudățenia mărimii eșantionului într-o singură dimensiune.)

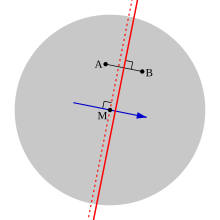
Dovadă . Vedeți diagrama, în care discul gri reprezintă distribuția alegătorului ca uniformă pe un cerc și M este mediana în toate direcțiile. Fie A și B doi candidați, dintre care A este cu atât mai aproape de mediană. Atunci alegătorii care se clasează pe A peste B sunt tocmai cei din stânga (adică partea „A”) a liniei roșii solide; și din moment ce A este mai aproape decât B de M, mediana este, de asemenea, la stânga acestei linii.

O distribuție fără mediană în toate direcțiile

Acum, deoarece M este o mediană în toate direcțiile, aceasta coincide cu mediana unidimensională în cazul particular al direcției arătate de săgeata albastră, care este perpendiculară pe linia roșie continuă. Astfel, dacă trasăm o linie roșie ruptă prin M, perpendicular pe săgeata albastră, atunci putem spune că jumătate dintre alegători se află la stânga acestei linii. Dar, din moment ce această linie este ea însăși la stânga liniei roșii solide, rezultă că mai mult de jumătate dintre alegători vor clasa A peste B.

Este ușor să construim distribuții electorale care nu au o mediană în toate direcțiile. Cel mai simplu exemplu constă într-o distribuție limitată la 3 puncte care nu se află în linie dreaptă, cum ar fi 1, 2 și 3 în a doua diagramă. Fiecare locație electorală coincide cu mediana sub un anumit set de proiecții unidimensionale. Dacă A, B și C sunt candidații, atunci „1” va vota ABC, „2” va vota BCA și „3” va vota CAB, oferind un ciclu Condorcet. Acesta este subiectul teoremei McKelvey – Schofield .

Relația dintre mediana în toate direcțiile și mediana geometrică

Ori de câte ori există o mediană omnidirecțională unică, aceasta determină rezultatul metodelor de votare Condorcet. În același timp, mediana geometrică poate fi identificată ca fiind câștigătorul ideal al unei alegeri de preferințe clasate (a se vedea Comparația sistemelor electorale ). Prin urmare, este important să cunoaștem relația dintre cei doi. De fapt, ori de câte ori există o mediană în toate direcțiile (cel puțin pentru cazul distribuțiilor discrete), aceasta coincide cu mediana geometrică.

Diagrama pentru lemă

Lemă . Ori de câte ori o distribuție discretă are o M mediană  în toate direcțiile, punctele de date care nu sunt situate la M   trebuie să vină în perechi echilibrate ( A , A  ') de ambele părți ale lui M   cu proprietatea că A  -  M  -  A  ' este o linie dreaptă ( adică nu ca A  0  -  M  -  A  2 din diagramă).

Dovadă . Acest rezultat a fost dovedit algebric de Charles Plott în 1967. Aici oferim o demonstrație geometrică simplă prin contradicție în două dimensiuni.

Să presupunem, dimpotrivă, că există un set de puncte A i care au M   ca mediană în toate direcțiile, dar pentru care punctele care nu coincid cu M   nu vin în perechi echilibrate. Apoi, putem elimina din acest set orice puncte la M și orice perechi echilibrate despre M , fără ca M   să înceteze să fie o mediană în orice direcție; deci M   rămâne o mediană omnidirecțională.

În cazul în care numărul de puncte rămase este impar, atunci putem trage cu ușurință o linie prin M   astfel încât majoritatea punctelor se află pe o parte a acesteia, în contradicție cu proprietatea median al M .

Dacă numărul este par, să spunem 2 n , atunci putem eticheta punctele A  0 , A 1 , ... în sensul acelor de ceasornic despre M   începând din orice punct (vezi diagrama). Fie θ unghiul subtins de arc de la M  - A  0 la M  - A n . Atunci dacă θ <180 ° așa cum se arată, putem trasa o linie similară cu linia roșie ruptă prin M   care are majoritatea punctelor de date pe o parte a acesteia, contrazicând din nou proprietatea mediană a lui M  ; întrucât dacă θ> 180 ° același lucru se aplică cu majoritatea punctelor de pe cealaltă parte. Și dacă θ = 180 °, atunci A  0 și A n formează o pereche echilibrată, contrazicând o altă presupunere.    

Teorema . Ori de câte ori o distribuție discretă are o mediană M   în toate direcțiile, aceasta coincide cu mediana sa geometrică.

Dovadă . Suma distanțelor de la orice punct P   la un set de puncte de date în perechi echilibrate ( A , A  ') este suma lungimilor A  -  P  -  A  '. Fiecare lungime individuală a acestei forme este minimizat peste P   atunci când linia este dreaptă, așa cum se întâmplă atunci când P   coincide cu M . Suma distanțelor de la P   la orice puncte de date situate la M   este, de asemenea, minimizată atunci când P   și M   coincid. Astfelsuma distanțelor de la puncteledate către P   este minimizat când P   coincide cu M  .

Legea Hotelling

Afirmația mai informală - modelul votantului median - este legată de „principiul diferențierii minime” a lui Harold Hotelling , cunoscut și sub numele de „ legea lui Hotelling ”. Se afirmă că politicienii gravitează spre poziția ocupată de votantul median, sau mai general spre poziția favorizată de sistemul electoral. A fost prezentat pentru prima dată (ca observație, fără nicio pretenție de rigoare) de Hotelling în 1929.

Hotelling a văzut comportamentul politicienilor prin ochii unui economist. El a fost surprins de faptul că magazinele care vând un anumit bun se adună adesea în aceeași parte a orașului și a văzut acest lucru ca fiind analog convergența partidelor politice. În ambele cazuri, poate fi o politică rațională pentru maximizarea cotei de piață .

Ca și în cazul oricărei caracterizări a motivației umane, aceasta depinde de factori psihologici care nu sunt ușor previzibili și este supusă multor excepții. De asemenea, este condiționat de sistemul de vot: politicienii nu vor converge la votantul median decât dacă procesul electoral o face. Dacă un proces electoral acordă mai multă greutate alegătorilor din mediul rural decât alegătorilor din mediul urban, atunci partidele vor converge probabil către politici care favorizează zonele rurale, mai degrabă decât către adevărata mediană.

Utilizări ale teoremei electorale mediane

Teorema este valoroasă pentru lumina pe care o aruncă asupra optimității (și limitelor la optimitate) a anumitor sisteme de vot.

Valerio Dotti subliniază domenii mai largi de aplicare:

Median Voter Teorema dovedit a fi extrem de popular în literatura de economie politică. Principalul motiv este că poate fi adoptat pentru a obține implicații testabile cu privire la relația dintre unele caracteristici ale populației cu drept de vot și rezultatul politicii, făcând abstracție de alte caracteristici ale procesului politic.

El adaugă că ...

Rezultatul votantului mediu a fost aplicat unei varietăți incredibile de întrebări. Exemple sunt analiza relației dintre inegalitatea veniturilor și mărimea intervenției guvernamentale în politicile redistributive (Meltzer și Richard, 1981), studiul factorilor determinanți ai politicilor de imigrație (Razin și Sadka, 1999), a gradului de impozitare pe diferite legături de venituri (Bassetto și Benhabib, 2006) și multe altele.

Vezi si

Referințe

Lecturi suplimentare

Link extern