Buclă (matematică) - Curl (mathematics)

În calculul vectorial , bucla este un operator vector care descrie circulația infinitesimală a unui câmp vectorial în spațiul euclidian tridimensional . Bucla într-un punct al câmpului este reprezentată de un vector a cărui lungime și direcție denotă magnitudinea și axa circulației maxime. Bucla unui câmp este definită formal ca densitatea de circulație în fiecare punct al câmpului.

Un câmp vector a cărui buclă este zero se numește irotațional . Bucla este o formă de diferențiere pentru câmpurile vectoriale. Forma corespunzătoare a teoremei fundamentale a calculului este teorema lui Stokes , care leagă integralul de suprafață al buclei unui câmp vectorial cu integrala de linie a câmpului vectorial din jurul curbei de graniță.

Terminologia alternativă rotație sau de rotație Notațiile și alternative putregaiul F sau produsul încrucișată cu del operatorul (nabla) ∇ × F sunt uneori utilizate pentru ondularea F . Standardul ISO / IEC 80000-2 recomandă utilizarea putregaiului notațiile îngroșate, spre deosebire de ondulare notație.

Spre deosebire de gradient și divergență , bucla așa cum este formulată în calculul vectorial nu se generalizează pur și simplu la alte dimensiuni; unele generalizări sunt posibile, dar numai în trei dimensiuni bucla definită geometric a unui câmp vector este din nou un câmp vector. Această deficiență este o consecință directă a limitărilor calculului vectorial; atunci când este exprimat prin intermediul operatorului de calcul geometric, bucla se generalizează la toate dimensiunile. Circumstanța nefericită este similară cu cea care participă la produsul transversal tridimensional și într-adevăr conexiunea se reflectă în notația ∇ × pentru buclă.

Numele „buclă” a fost sugerat pentru prima dată de James Clerk Maxwell în 1871, dar se pare că conceptul a fost folosit pentru prima dată în construcția teoriei câmpului optic de către James MacCullagh în 1839.

Definiție

Bucla unui câmp vector F , notată cu ondulația F , sau ∇ × F , sau putregaiul F , într-un punct este definită în termeni de proiecție pe diferite linii prin punct. Dacă este un vector unitar, proiecția buclei lui F pe este definită ca fiind valoarea limitativă a unei linii închise integrale într-un plan ortogonal la împărțită la aria închisă, deoarece calea de integrare este contractată în jurul punctului. ${\ displaystyle \ mathbf {\ hat {n}}}$${\ displaystyle \ mathbf {\ hat {n}}}$${\ displaystyle \ mathbf {\ hat {n}}}$

Operatorul de curl mapează funcții continuu diferențiabile f  : R ³ → R ³ la funcții continue g  : R ³ → R ³ și, în special, mapează funcțiile C ^k în R ³ până la C ^{k −1} funcții în R ³ .

Implicit, bucla este definită într-un punct p ca

${\ displaystyle (\ nabla \ times \ mathbf {F}) (p) \ cdot \ mathbf {\ hat {n}} \ {\ overset {\ underset {\ mathrm {def}} {}} {{} = { }}} \ lim _ {A \ to 0} {\ frac {1} {| A |}} \ oint _ {C} \ mathbf {F} \ cdot \ mathrm {d} \ mathbf {r}}$

unde integrala de linie este calculată de-a lungul limitei C a zonei A în cauză, | A | fiind magnitudinea zonei. Această ecuație definește proiecția buclei lui F pe . Suprafețele infinitesimale delimitate de C au ca normalitate . C este orientat prin regula din dreapta . ${\ displaystyle \ mathbf {\ hat {n}}}$${\ displaystyle \ mathbf {\ hat {n}}}$

Formula de mai sus înseamnă că bucla unui câmp vector este definită ca densitatea de zonă infinitesimală a circulației acelui câmp. La această definiție se potrivește în mod natural

• teorema Kelvin-Stokes , ca o formulă globală care corespunde definiției și
• următoarea definiție „ușor de memorat” a buclei în coordonate ortogonale curvilinee , de ex. în coordonate carteziene , sferice , cilindrice sau chiar eliptice sau parabolice :

  ${\ displaystyle {\ begin {align} & (\ operatorname {curl} \ mathbf {F}) _ {1} = {\ frac {1} {h_ {2} h_ {3}}} \ left ({\ frac {\ partial (h_ {3} F_ {3})} {\ partial u_ {2}}} - {\ frac {\ partial (h_ {2} F_ {2})} {\ partial u_ {3}}} \ right), \\ [5pt] & (\ operatorname {curl} \ mathbf {F}) _ {2} = {\ frac {1} {h_ {3} h_ {1}}} \ left ({\ frac {\ partial (h_ {1} F_ {1})} {\ partial u_ {3}}} - {\ frac {\ partial (h_ {3} F_ {3})} {\ partial u_ {1}}} \ right), \\ [5pt] & (\ operatorname {curl} \ mathbf {F}) _ {3} = {\ frac {1} {h_ {1} h_ {2}}} \ left ({\ frac {\ partial (h_ {2} F_ {2})} {\ partial u_ {1}}} - {\ frac {\ partial (h_ {1} F_ {1})} {\ partial u_ {2}}} \ dreapta). \ end {align}}}$

Ecuația pentru fiecare componentă (bucla F ) _k poate fi obținută schimbând fiecare apariție a unui indiciu 1, 2, 3 în permutare ciclică: 1 → 2, 2 → 3 și 3 → 1 (unde indicii reprezintă indicii relevanți) .

Dacă ( x ₁ , x ₂ , x ₃ ) sunt coordonatele carteziene și ( u ₁ , u ₂ , u ₃ ) sunt coordonatele ortogonale, atunci

${\ displaystyle h_ {i} = {\ sqrt {\ left ({\ frac {\ partial x_ {1}} {\ partial u_ {i}}} \ right) ^ {2} + \ left ({\ frac { \ partial x_ {2}} {\ partial u_ {i}}} \ right) ^ {2} + \ left ({\ frac {\ partial x_ {3}} {\ partial u_ {i}}} \ right) ^ {2}}}}$

este lungimea vectorului de coordonate corespunzător lui u _i . Celelalte două componente ale buclei rezultă din permutarea ciclică a indicilor : 3,1,2 → 1,2,3 → 2,3,1.

Interpretare intuitivă

Să presupunem că câmpul vectorial descrie câmpul de viteză al unui flux de fluid (cum ar fi un rezervor mare de lichid sau gaz ) și o bilă mică este situată în interiorul fluidului sau gazului (centrul mingii fiind fixat într-un anumit punct). Dacă bila are o suprafață aspră, fluidul care curge pe lângă ea o va face să se rotească. Axa de rotație (orientată conform regulii mâinii drepte) indică direcția buclei câmpului în centrul mingii, iar viteza unghiulară a rotației este jumătate din magnitudinea buclei în acest punct.

Bucla vectorului în orice punct este dată de rotația unei zone infinitesimale în planul xy (pentru componenta z- axă a buclei), planul zx (pentru componenta y- axă a buclei) și planul yz (pentru componenta axei x a vectorului curl). Acest lucru poate fi văzut clar în exemplele de mai jos.

Utilizare

În practică, definiția de mai sus este rareori utilizată, deoarece în practic toate cazurile, operatorul de curl poate fi aplicat folosind un set de coordonate curvilinee , pentru care au fost derivate reprezentări mai simple.

Notația ∇ × F își are originea în similitudinile cu produsul transversal tridimensional și este utilă ca mnemonică în coordonatele carteziene dacă ∇ este luat ca operator diferențial vectorial del . O astfel de notație care implică operatori este comună în fizică și algebră .

Extins în coordonate carteziene tridimensionale (vezi Del în coordonate cilindrice și sferice pentru reprezentări de coordonate sferice și cilindrice ), ∇ × F este, pentru F compus din [ F _x , F _y , F _z ] (unde indicii indică componentele vectorul, nu derivate parțiale):

${\ displaystyle \ nabla \ times \ mathbf {F} = {\ begin {vmatrix} {\ boldsymbol {\ hat {\ imath}}} și {\ boldsymbol {\ hat {\ jmath}}} & {\ boldsymbol {\ hat {k}}} \\ [5pt] {\ dfrac {\ partial} {\ partial x}} și {\ dfrac {\ partial} {\ partial y}} și {\ dfrac {\ partial} {\ partial z }} \\ [10pt] F_ {x} & F_ {y} & F_ {z} \ end {vmatrix}}}$

unde i , j și k sunt versorii pentru x -, y - și z -axes respectiv. Aceasta se extinde după cum urmează:

${\ displaystyle \ nabla \ times \ mathbf {F} = \ left ({\ frac {\ partial F_ {z}} {\ partial y}} - {\ frac {\ partial F_ {y}} {\ partial z} } \ right) {\ boldsymbol {\ hat {\ imath}}} + \ left ({\ frac {\ partial F_ {x}} {\ partial z}} - {\ frac {\ partial F_ {z}} { \ partial x}} \ right) {\ boldsymbol {\ hat {\ jmath}}} + \ left ({\ frac {\ partial F_ {y}} {\ partial x}} - {\ frac {\ partial F_ { x}} {\ partial y}} \ right) {\ boldsymbol {\ hat {k}}} = {\ begin {bmatrix} {\ frac {\ partial F_ {z}} {\ partial y}} - {\ frac {\ partial F_ {y}} {\ partial z}} \\ {\ frac {\ partial F_ {x}} {\ partial z}} - {\ frac {\ partial F_ {z}} {\ partial x }} \\ {\ frac {\ partial F_ {y}} {\ partial x}} - {\ frac {\ partial F_ {x}} {\ partial y}} \ end {bmatrix}}}$

Deși este exprimat în termeni de coordonate, rezultatul este invariant în rotațiile corespunzătoare ale axelor de coordonate, dar rezultatul se inversează în reflecție.

Într-un sistem general de coordonate, bucla este dată de

${\ displaystyle (\ nabla \ times \ mathbf {F}) ^ {k} = {\ frac {1} {\ sqrt {g}}} \ varepsilon ^ {k \ ell m} \ nabla _ {\ ell} F_ {m}}$

unde ε reprezintă tensorul Levi-Civita , ∇ derivatul covariantă , este Jacobian și convenția însumare Einstein implică faptul că indicii repetate sunt însumate peste. Datorită simetriei simbolurilor Christoffel care participă la derivata covariantă, această expresie se reduce la derivata parțială: ${\ displaystyle {\ sqrt {g}}}$

${\ displaystyle (\ nabla \ times \ mathbf {F}) = {\ frac {1} {\ sqrt {g}}} \ mathbf {R} _ {k} \ varepsilon ^ {k \ ell m} \ partial _ {l} F_ {m}}$

unde R _k sunt vectorii de bază locale. În mod echivalent, folosind derivatul exterior , bucla poate fi exprimată ca:

${\ displaystyle \ nabla \ times \ mathbf {F} = \ left (\ star {\ big (} {\ mathrm {d}} \ mathbf {F} ^ {\ flat} {\ big)} \ right) ^ { \ sharp}}$

Aici ♭ și ♯ sunt izomorfismele muzicale și ★ este operatorul stelelor Hodge . Această formulă arată cum se calculează bucla lui F în orice sistem de coordonate și cum se extinde bucla la orice colector Riemannian tridimensional orientat . Deoarece acest lucru depinde de o alegere de orientare, ondularea este o operație chirală . Cu alte cuvinte, dacă orientarea este inversă, atunci și direcția buclei este inversată.

Exemple

Exemplul 1

Câmpul vector

${\ displaystyle \ mathbf {F} (x, y, z) = y {\ boldsymbol {\ hat {\ imath}}} - x {\ boldsymbol {\ hat {\ jmath}}}}$

poate fi descompus ca

${\ displaystyle \ mathbf {F} _ {x} = y, \ mathbf {F} _ {y} = - x, \ mathbf {F} _ {z} = 0.}$

La inspecția vizuală, câmpul poate fi descris ca „rotativ”. Dacă vectorii câmpului ar reprezenta o forță liniară care acționează asupra obiectelor prezente în acel punct și un obiect ar fi plasat în interiorul câmpului, obiectul ar începe să se rotească în sensul acelor de ceasornic în jurul său. Acest lucru este valabil indiferent de locul în care este plasat obiectul.

Calculul buclei:

${\ displaystyle \ nabla \ times \ mathbf {F} = 0 {\ boldsymbol {\ hat {\ imath}}} + 0 {\ boldsymbol {\ hat {\ jmath}}} + \ left ({\ frac {\ partial } {\ partial x}} (- x) - {\ frac {\ partial} {\ partial y}} y \ right) {\ boldsymbol {\ hat {k}}} = - 2 {\ boldsymbol {\ hat { k}}}}$

Câmpul vectorial rezultat care descrie bucla ar fi în toate punctele îndreptat în direcția z negativă . Rezultatele acestei ecuații se aliniază cu ceea ce s-ar fi putut prezice folosind regula mâinii drepte folosind un sistem de coordonate dreptaci . Fiind un câmp vectorial uniform, obiectul descris anterior ar avea aceeași intensitate de rotație indiferent de locul în care a fost plasat.

Exemplul 2

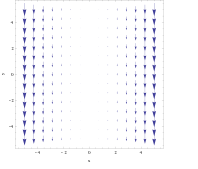
Pentru câmpul vector

${\ displaystyle \ mathbf {F} (x, y, z) = - x ^ {2} {\ boldsymbol {\ hat {\ jmath}}}}$

bucla nu este la fel de evidentă din grafic. Totuși, luând obiectul din exemplul anterior și plasându-l oriunde pe linia x = 3 , forța exercitată pe partea dreaptă ar fi puțin mai mare decât forța exercitată pe stânga, determinând rotirea acestuia în sensul acelor de ceasornic. Folosind regula mâinii drepte, se poate prezice că bucla rezultată ar fi dreaptă în direcția z negativă . Invers, dacă este plasat pe x = −3 , obiectul s-ar roti în sens invers acelor de ceasornic și regula din dreapta ar avea ca rezultat o direcție z pozitivă .

Calculul buclei:

${\ displaystyle {\ nabla} \ times \ mathbf {F} = 0 {\ boldsymbol {\ hat {\ imath}}} + 0 {\ boldsymbol {\ hat {\ jmath}}} + {\ frac {\ partial} {\ partial x}} \ left (-x ^ {2} \ right) {\ boldsymbol {\ hat {k}}} = - 2x {\ boldsymbol {\ hat {k}}}.}$

Bucla indică în direcția z negativă atunci când x este pozitiv și invers. În acest câmp, intensitatea rotației ar fi mai mare pe măsură ce obiectul se îndepărtează de planul x = 0 .

Exemple descriptive

• Într-un câmp vector care descrie viteza liniară a fiecărei părți a unui disc rotativ, bucla are aceeași valoare în toate punctele.
• Dintre cele patru ecuații ale lui Maxwell , două - legea Faraday și legea lui Ampère - pot fi exprimate compact folosind bucl. Legea lui Faraday afirmă că bucla unui câmp electric este egală cu opusul ratei de schimbare a timpului câmpului magnetic, în timp ce legea lui Ampère leagă bucla câmpului magnetic de curent și viteza de schimbare a câmpului electric.

Identități

În coordonatele curvilinei generale (nu numai în coordonatele carteziene), bucla unui produs încrucișat de câmpuri vectoriale v și F poate fi demonstrată a fi

${\ displaystyle \ nabla \ times \ left (\ mathbf {v \ times F} \ right) = {\ Big (} \ left (\ mathbf {\ nabla \ cdot F} \ right) + \ mathbf {F \ cdot \ nabla} {\ Big)} \ mathbf {v} - {\ Big (} \ left (\ mathbf {\ nabla \ cdot v} \ right) + \ mathbf {v \ cdot \ nabla} {\ Big)} \ mathbf {F} \.}$

Schimbând operatorul câmpului v și ∇ , ajungem la produsul încrucișat al unui câmp vector cu bucla unui câmp vector:

${\ displaystyle \ mathbf {v \ \ times} \ left (\ mathbf {\ nabla \ times F} \ right) = \ nabla _ {\ mathbf {F}} \ left (\ mathbf {v \ cdot F} \ right ) - \ left (\ mathbf {v \ cdot \ nabla} \ right) \ mathbf {F} \,}$

unde ∇ _F este notația Feynman, care consideră doar variația datorată câmpului vector F (adică, în acest caz, v este tratat ca fiind constant în spațiu).

Un alt exemplu este ondularea unei bucle a unui câmp vector. Se poate arăta că în coordonatele generale

${\ displaystyle \ nabla \ times \ left (\ mathbf {\ nabla \ times F} \ right) = \ mathbf {\ nabla} (\ mathbf {\ nabla \ cdot F}) - \ nabla ^ {2} \ mathbf { F} \,}$

și această identitate definește Laplacianul vectorul de F , simbolizată ∇ ² F .

Curl a gradientului de orice câmp scalar φ este întotdeauna vectorul de zero câmp

${\ displaystyle \ nabla \ times (\ nabla \ varphi) = {\ boldsymbol {0}}}$

care rezultă din antisimetria din definiția buclei și din simetria derivatelor secundare .

Dacă φ este o funcție cu valoare scalară și F este un câmp vectorial, atunci

${\ displaystyle \ nabla \ times (\ varphi \ mathbf {F}) = \ nabla \ varphi \ times \ mathbf {F} + \ varphi \ nabla \ times \ mathbf {F}}$

Generalizări

Operațiile de calcul vectorial ale gradului , curlului și divului sunt cel mai ușor generalizate în contextul formelor diferențiale, care implică un număr de pași. Pe scurt, ele corespund derivatelor formelor 0, formelor 1 și respectiv formelor 2. Interpretarea geometrică a curlului ca rotație corespunde identificării bivectori (2-vectori) în 3 dimensiuni cu algebra Lie ortogonală specială (3) a rotațiilor infinitezimale (în coordonate, matrici 3 × 3 simetrice înclinate), în timp ce reprezentarea rotațiilor prin vectori corespunde la identificarea 1-vectori (echivalent, 2-vectori) și (3) , toate acestea fiind spații tridimensionale. ${\ displaystyle {\ mathfrak {so}}}$${\ displaystyle {\ mathfrak {so}}}$

Forme diferențiale

În 3 dimensiuni, o formă diferențială 0 este pur și simplu o funcție f ( x , y , z ) ; o formă diferențială 1 este următoarea expresie, unde coeficienții sunt funcții:

${\ displaystyle a_ {1} \, dx + a_ {2} \, dy + a_ {3} \, dz;}$

o formă diferențială 2 este suma formală, din nou cu coeficienți de funcție:

${\ displaystyle a_ {12} \, dx \ wedge dy + a_ {13} \, dx \ wedge dz + a_ {23} \, dy \ wedge dz;}$

și o formă diferențială 3 este definită de un singur termen cu o funcție ca coeficient:

${\ displaystyle a_ {123} \, dx \ wedge dy \ wedge dz.}$

(Aici un -coefficients sunt functii reale de trei variabile, „produse de pană“, de exemplu , dx ∧ dy , poate fi interpretat ca un fel de elemente din zona orientate, dx ∧ dy = - dy ∧ dx etc.)

Derivatul exterior al unui k forma a în R ³ este definit ca ( k + 1) , în forma p de mai sus și în R ⁿ , dacă, de exemplu,

${\ displaystyle \ omega ^ {(k)} = \ sum _ {\ scriptstyle {i_ {1} <i_ {2} <\ cdots <i_ {k}} \ atop \ forall \ scriptstyle {i _ {\ nu} \ în 1, \ ldots, n}} a_ {i_ {1}, \ ldots, i_ {k}} \, dx_ {i_ {1}} \ wedge \ cdots \ wedge dx_ {i_ {k}},}$

atunci derivata exterioară d duce la

${\ displaystyle d \ omega ^ {(k)} = \ sum _ {\ scriptstyle {j = 1} \ atop \ scriptstyle {i_ {1} <\ cdots <i_ {k}}} ^ {n} {\ frac {\ partial a_ {i_ {1}, \ ldots, i_ {k}}} {\ partial x_ {j}}} \, dx_ {j} \ wedge dx_ {i_ {1}} \ wedge \ cdots \ wedge dx_ {i_ {k}}.}$

Derivatul exterior al unei forme 1 este, prin urmare, o formă 2, iar cea a unei forme 2 este o formă 3. Pe de altă parte, datorită interschimbabilității derivatelor mixte, de exemplu din cauza

${\ displaystyle {\ frac {\ partial ^ {2}} {\ partial x \, \ partial y}} = {\ frac {\ partial ^ {2}} {\ partial y \, \ partial x}},}$

aplicarea dublă a derivatei exterioare duce la 0.

Astfel, denotând spațiul formelor k cu Ω ^k ( R ³ ) și derivatul exterior cu d se obține o succesiune:

${\ displaystyle 0 \, {\ overset {d} {\ longrightarrow}} \; \ Omega ^ {0} \ left (\ mathbb {R} ^ {3} \ right) \, {\ overset {d} {\ longrightarrow}} \; \ Omega ^ {1} \ left (\ mathbb {R} ^ {3} \ right) \, {\ overset {d} {\ longrightarrow}} \; \ Omega ^ {2} \ left ( \ mathbb {R} ^ {3} \ right) \, {\ overset {d} {\ longrightarrow}} \; \ Omega ^ {3} \ left (\ mathbb {R} ^ {3} \ right) \, {\ overset {d} {\ longrightarrow}} \, 0.}$

Aici Ω ^k ( R ⁿ ) este spațiul secțiunilor algebrei exterioare Λ ^k ( R ⁿ ) pachet vectorial peste R ⁿ , a cărui dimensiune este coeficientul binomial (ⁿ
_k) ; rețineți căΩ ^k ( R ³ ) = 0pentru k > 3sau k <0. Scriind doar dimensiuni, se obține un rând dintriunghiul lui Pascal:

0 → 1 → 3 → 3 → 1 → 0;

fibrele unidimensionale corespund câmpurilor scalare, iar fibrele tridimensionale câmpurilor vectoriale, așa cum este descris mai jos. Modulo identificări adecvate, cele trei apariții netiviale ale derivatei exterioare corespund gradului, buclei și div.

Formele diferențiale și diferențialul pot fi definite pe orice spațiu euclidian, sau într-adevăr pe orice varietate, fără nicio noțiune de metrică riemanniană. Pe un colector riemanniene , sau mai general colector pseudo riemanniene , k -forms poate fi identificat cu k -vector câmpuri ( k -forms sunt k câmpurile -covector și o metrică pseudo riemannian oferă izomorfism între vectori și covectors) și pe un spațiu vectorial orientat cu o formă nedegenerată (un izomorfism între vectori și covectori), există un izomorfism între k -vectori și ( n - k ) -vectori; în special pe (spațiul tangent al) unei varietăți orientate pseudo-Riemanniene. Astfel, pe o varietate orientată pseudo-Riemanniană, se pot schimba k- forme, k- câmpuri vectoriale, ( n - k ) -forme și ( n - k ) -câmpuri vectoriale; aceasta este cunoscută sub numele de dualitate Hodge . Concret, pe R ³ acest lucru este dat de:

• 1-forme și 1-câmpuri vectoriale: forma 1 a _x dx + a _y dy + a _z dz corespunde câmpului vectorial ( a _x , a _y , a _z ) .
• 1-forme și 2-forme: unul înlocuiește dx cu cantitatea duală dy ∧ dz (adică omiteți dx ) și, la fel, având grijă de orientare: dy corespunde dz ∧ dx = - dx ∧ dz , iar dz corespunde dx ∧ dy . Astfel forma a _x dx + a _y dy + a _z dz corespunde „formei duale” a _z dx ∧ dy + a _y dz ∧ dx + a _x dy ∧ dz .

Astfel, identificarea formelor 0 și 3-forme cu câmpuri scalare și 1-forme și 2-forme cu câmpuri vectoriale:

• grad ia un câmp scalar (0-formă) într-un câmp vector (1-formă);
• curl ia un câmp vector (1 formă) într-un câmp pseudovector (2 formă);
• div ia un câmp pseudovector (2 forme) într-un câmp pseudoscalar (3 forme)

Pe de altă parte, faptul că d ² = 0 corespunde identităților

${\ displaystyle \ nabla \ times (\ nabla f) = 0}$

pentru orice câmp scalar f și

${\ displaystyle \ nabla \ cdot (\ nabla \ times \ mathbf {v}) = 0}$

pentru orice câmp vectorial v .

Grad și div generalizează la toate varietățile pseudo-riemanniene orientate, cu aceeași interpretare geometrică, deoarece spațiile formelor 0 și formelor n din fiecare punct sunt întotdeauna 1-dimensionale și pot fi identificate cu câmpuri scalare, în timp ce spațiile 1 -formele și ( n - 1) -formele sunt întotdeauna fibre n -dimensionale și pot fi identificate cu câmpuri vectoriale.

Curl nu se generalizează în acest fel la 4 sau mai multe dimensiuni (sau până la 2 sau mai puține dimensiuni); în 4 dimensiuni dimensiunile sunt

0 → 1 → 4 → 6 → 4 → 1 → 0;

deci bucla unui câmp cu 1 vector (în formă de fibră 4-dimensional) este un câmp cu 2 vectori , care în fiecare punct aparține spațiului vectorial cu 6 dimensiuni și deci unul are

${\ displaystyle \ omega ^ {(2)} = \ sum _ {i <k = 1,2,3,4} a_ {i, k} \, dx_ {i} \ wedge dx_ {k},}$

care produce o sumă de șase termeni independenți și nu poate fi identificat cu un câmp cu 1 vector. Nici nu se poate trece în mod semnificativ de la un câmp cu 1 vector la un câmp cu 2 vectori la un câmp cu 3 vectori (4 → 6 → 4), deoarece luând diferențialul de două ori se obține zero ( d ² = 0 ). Astfel, nu există o funcție de curl de la câmpuri vectoriale la câmpuri vectoriale în alte dimensiuni care apar astfel.

Cu toate acestea, se poate defini o buclă a unui câmp vector ca un câmp cu 2 vectori în general, așa cum este descris mai jos.

Ondulați geometric

2-vectori corespund puterii exterioare Λ ² V ; în prezența unui produs interior, în coordonate acestea sunt matricele înclinate-simetrice, care sunt considerate geometric ca algebra de minte ortogonală specială ( V ) a rotațiilor infinitezimale. Aceasta are (${\ displaystyle {\ mathfrak {so}}}$ⁿ
₂) = 1/2n ( n - 1) dimensiuni și permite interpretarea diferențialului unui câmp cu 1 vector ca rotații infinitezimale. Numai în 3 dimensiuni (sau trivial în 0 dimensiuni) n =1/2n ( n - 1) , care este cel mai elegant și obișnuit caz. În 2 dimensiuni, bucla unui câmp vector nu este un câmp vector, ci o funcție, deoarece rotațiile bidimensionale sunt date de un unghi (un scalar - este necesară o orientare pentru a alege dacă una contează rotațiile în sensul acelor de ceasornic sau în sens invers acelor de ceasornic ca pozitive); aceasta nu este div, ci este mai degrabă perpendiculară pe ea. În 3 dimensiuni, bucla unui câmp vector este un câmp vector, așa cum este familiar (în dimensiunile 1 și 0, bucla unui câmp vector este 0, deoarece nu există 2-vectori non-banali), în timp ce în 4 dimensiuni, bucla de un câmp vector este, geometric, în fiecare punct un element al algebrei Lie în 6 dimensiuni. ${\ displaystyle {\ mathfrak {so}} (4)}$

Bucla unui câmp vectorial tridimensional care depinde doar de 2 coordonate (să zicem x și y ) este pur și simplu un câmp vector vertical (în direcția z ) a cărui magnitudine este bucla câmpului vectorial bidimensional, ca în exemple Pe aceasta pagina.

Considerând curlul ca un câmp cu 2 vectori (un 2-tensor antisimetric) a fost folosit pentru a generaliza calculul vectorial și fizica asociată la dimensiuni superioare.

Invers

În cazul în care divergența unui câmp vector V este zero, există un câmp vector W astfel încât V = bucla ( W ) . Acesta este motivul pentru care câmpul magnetic , caracterizat prin divergență zero, poate fi exprimat ca o buclă a unui potențial magnetic magnetic .

Dacă W este un câmp vector cu bucla ( W ) = V , atunci adăugarea oricărui câmp vector gradient grad (  f  ) la W va avea ca rezultat un alt câmp vectorial W + grad (  f  ) astfel încât bucla ( W + grad (  f  )) = V , de asemenea. Acest lucru poate fi rezumat spunând că bucla inversă a unui câmp vectorial tridimensional poate fi obținută până la un câmp irotațional necunoscut cu legea Biot – Savart .

Vezi si

O parte dintr-o serie de articole despre
Calcul
Teorema fundamentală Regula integrală Leibniz Limitele funcțiilor Continuitate Teorema valorii medii Teorema lui Rolle
Diferenţial Definiții Derivată  ( generalizări ) Diferenţial infinitezimal a unei funcții total Concepte Notare de diferențiere A doua derivată Diferențierea implicită Diferențierea logaritmică Tarife aferente Teorema lui Taylor Reguli și identități Sumă Produs Lanţ Putere Coeficient Regula L'Hôpital Invers Generalul Leibniz Formula lui Faà di Bruno Reynolds
Integral Liste de integrale Transformare integrală Definiții Antiderivativ Integral  ( necorespunzător ) Integrala Riemann Integrarea Lebesgue Integrarea conturului Integrală a funcțiilor inverse Integrarea de către Părți Discuri Cochilii cilindrice Înlocuire  ( trigonometrică , Weierstrass , Euler ) Formula lui Euler Fracții parțiale Schimbarea ordinii Formule de reducere Diferențierea sub semnul integral Algoritmul Risch
Serie Geometric  ( aritmetico-geometric ) Armonic Alternativ Putere Binom Taylor Teste de convergență Limita Summand (test de termen) Raport Rădăcină Integral Comparație directă Limitează comparația Seria alternativă Condensare cauchy Dirichlet Abel
Vector Gradient Divergenţă Răsuci Laplacian Derivată direcțională Identități Teoreme Gradient Verdeaţă Stokes ' Divergenţă generalizat Stokes
Multivariabil Formalisme Matrice Tensor Exterior Geometric Definiții Derivată parțială Integrală multiplă Integrală de linie Integrală de suprafață Integrală de volum Jacobian Hessian
De specialitate Fracțional Malliavin Stochastic Variații
Diverse Precalcul Istorie Glosar Lista subiectelor Integrare albină Analiză
v t e

• Descompunerea Helmholtz
• Del în coordonate cilindrice și sferice
• Vorticitate

Referințe

Lecturi suplimentare

• Korn, Granino Arthur și Theresa M. Korn (ianuarie 2000). Manual matematic pentru oameni de știință și ingineri: definiții, teoreme și formule pentru referință și revizuire . New York: publicațiile Dover. pp. 157–160. ISBN 0-486-41147-8.
• Schey, HM (1997). Div, Grad, Curl și toate acestea: un text informal despre calculul vectorial . New York: Norton. ISBN 0-393-96997-5.

linkuri externe

• „Curl” , Enciclopedia Matematicii , EMS Press , 2001 [1994]
• „Calcul Vector: Înțelegerea circulației și a curbării - mai bine explicat” . betterexplained.com . Adus 09-11-2020 .
• „Divergență și curl: limbajul ecuațiilor lui Maxwell, fluxului de fluid și multe altele” . 21 iunie 2018 - prin YouTube .