Cerc circumscris - Circumscribed circle

În geometrie , cercul circumscris sau circumcercul unui poligon este un cerc care trece prin toate vârfurile poligonului. Centrul acestui cerc se numește circumcenter, iar raza acestuia se numește circumradius .

Nu fiecare poligon are un cerc circumscris. Un poligon care are unul se numește poligon ciclic , sau uneori poligon conciclic, deoarece vârfurile sale sunt conciclice . Toate triunghiurile , toate poligoanele simple regulate , toate dreptunghiurile , toate trapezele izoscele și toate zmeurile drepte sunt ciclice.

O noțiune înrudită este cea a unui cerc de limitare minimă , care este cel mai mic cerc care conține complet poligonul din interiorul acestuia, dacă centrul cercului se află în interiorul poligonului. Fiecare poligon are un cerc de limitare minim unic, care poate fi construit de un algoritm de timp liniar . Chiar dacă un poligon are un cerc circumscris, acesta poate fi diferit de cercul său de limitare minimă. De exemplu, pentru un triunghi obtuz , cercul de limitare minim are cea mai lungă latură ca diametru și nu trece prin vârful opus.

Triunghiuri

Toate triunghiurile sunt ciclice; adică fiecare triunghi are un cerc circumscris.

Construcție de linie dreaptă și busolă

Circumcentrul unui triunghi poate fi construit trasând oricare dintre cele trei bisectoare perpendiculare . Pentru trei puncte necoliniare, aceste două linii nu pot fi paralele, iar circumcentrul este punctul în care se traversează. Orice punct de pe bisectoare este echidistant de cele două puncte pe care le bisectează, din care rezultă că acest punct, pe ambele bisectoare, este echidistant de la toate cele trei vârfuri triunghiulare. Circumradiusul este distanța de la acesta la oricare dintre cele trei vârfuri.

Construcție alternativă

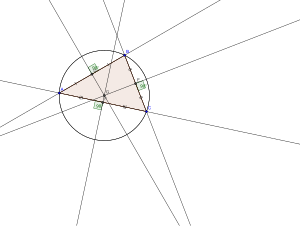
O metodă alternativă de determinare a circumcentrului este de a trasa oricare două linii fiecare plecând de la unul din vârfuri la un unghi cu latura comună, unghiul comun de plecare fiind de 90 ° minus unghiul vârfului opus. (În cazul în care unghiul opus este obtuz, trasarea unei linii la un unghi negativ înseamnă ieșirea în afara triunghiului.)

În navigația de coastă , circumcercul unui triunghi este uneori folosit ca o modalitate de a obține o linie de poziție folosind un sextant atunci când nu este disponibilă o busolă . Unghiul orizontal dintre două repere definește circumcercul pe care se află observatorul.

Ecuații de cerc

Coordonatele carteziene

În planul euclidian , este posibil să se dea explicit o ecuație a circumcercului în termenii coordonatelor carteziene ale vârfurilor triunghiului inscripționat. Să presupunem că

${\ displaystyle {\ begin {align} \ mathbf {A} & = (A_ {x}, A_ {y}) \\\ mathbf {B} & = (B_ {x}, B_ {y}) \\\ mathbf {C} & = (C_ {x}, C_ {y}) \ end {align}}}$

sunt coordonatele punctelor A , B și C . Circumscripția este apoi locul punctelor v = ( v _x ,  v _y ) în planul cartesian care îndeplinește ecuațiile

${\ displaystyle {\ begin {align} | \ mathbf {v} - \ mathbf {u} | ^ {2} & = r ^ {2} \\ | \ mathbf {A} - \ mathbf {u} | ^ { 2} & = r ^ {2} \\ | \ mathbf {B} - \ mathbf {u} | ^ {2} & = r ^ {2} \\ | \ mathbf {C} - \ mathbf {u} | ^ {2} & = r ^ {2} \ end {align}}}$

garantând că punctele A , B , C și v sunt toate la aceeași distanță r de centrul comun u al cercului. Folosind identitatea de polarizare , aceste ecuații se reduc la condiția ca matricea

${\ displaystyle {\ begin {bmatrix} | \ mathbf {v} | ^ {2} & - 2v_ {x} & - 2v_ {y} & - 1 \\ | \ mathbf {A} | ^ {2} & - 2A_ {x} & - 2A_ {y} & - 1 \\ | \ mathbf {B} | ^ {2} & - 2B_ {x} & - 2B_ {y} & - 1 \\ | \ mathbf {C} | ^ {2} & - 2C_ {x} & - 2C_ {y} & - 1 \ end {bmatrix}}}$

are un nucleu diferit de zero . Astfel circumcercul poate fi alternativ descris ca locusul zerourilor determinantului acestei matrici:

${\ displaystyle \ det {\ begin {bmatrix} | \ mathbf {v} | ^ {2} & v_ {x} & v_ {y} & 1 \\ | \ mathbf {A} | ^ {2} & A_ {x} & A_ { y} & 1 \\ | \ mathbf {B} | ^ {2} & B_ {x} & B_ {y} & 1 \\ | \ mathbf {C} | ^ {2} & C_ {x} & C_ {y} & 1 \ end { bmatrix}} = 0.}$

Folosind expansiunea cofactorului , let

${\ displaystyle {\ begin {align} S_ {x} & = {\ frac {1} {2}} \ det {\ begin {bmatrix} | \ mathbf {A} | ^ {2} & A_ {y} & 1 \ \ | \ mathbf {B} | ^ {2} & B_ {y} & 1 \\ | \ mathbf {C} | ^ {2} & C_ {y} & 1 \ end {bmatrix}}, \\ [5pt] S_ {y } & = {\ frac {1} {2}} \ det {\ begin {bmatrix} A_ {x} & | \ mathbf {A} | ^ {2} & 1 \\ B_ {x} & | \ mathbf {B } | ^ {2} & 1 \\ C_ {x} & | \ mathbf {C} | ^ {2} & 1 \ end {bmatrix}}, \\ [5pt] a & = \ det {\ begin {bmatrix} A_ { x} & A_ {y} & 1 \\ B_ {x} & B_ {y} & 1 \\ C_ {x} & C_ {y} & 1 \ end {bmatrix}}, \\ [5pt] b & = \ det {\ begin {bmatrix } A_ {x} & A_ {y} & | \ mathbf {A} | ^ {2} \\ B_ {x} & B_ {y} & | \ mathbf {B} | ^ {2} \\ C_ {x} & C_ {y} & | \ mathbf {C} | ^ {2} \ end {bmatrix}} \ end {align}}}$

avem apoi un | v | ² - 2 Sv - b = 0 unde S = ( S _x ,  S _y ) și - presupunând că cele trei puncte nu erau într-o linie (altfel circumcercul este acea linie care poate fi văzută și ca un cerc generalizat cu S la infinit ) - | v - S / a | ² = b / a + | S | ² / a ² , dând circumcentrul S / a și circumradiusul √ b / a + | S | ² / a ² . O abordare similară permite deducerea ecuației circumferei unui tetraedru .

Ecuația parametrică

Un vector unitate perpendicular pe planul care conține cercul este dat de

${\ displaystyle {\ widehat {n}} = {\ frac {(P_ {2} -P_ {1}) \ times (P_ {3} -P_ {1})} {| (P_ {2} -P_ { 1}) \ times (P_ {3} -P_ {1}) |}}.}$

Prin urmare, având în vedere raza, r , centru, P _c , un punct pe cerc, P ₀ și o unitate normală a planului care conține cercul , o ecuație parametrică a cercului care începe de la punctul P ₀ și continuă într-un mod pozitiv sens orientat (adică dreptaci ) despre este următorul: ${\ textstyle {\ widehat {n}}}$${\ displaystyle \ scriptstyle {\ widehat {n}}}$

${\ displaystyle \ mathrm {R} (s) = \ mathrm {P_ {c}} + \ cos \ left ({\ frac {\ mathrm {s}} {\ mathrm {r}}} \ right) (P_ { 0} -P_ {c}) + \ sin \ left ({\ frac {\ mathrm {s}} {\ mathrm {r}}} \ right) \ left [{\ widehat {n}} \ times (P_ { 0} -P_ {c}) \ dreapta].}$

Coordonate triliniare și barientrice

O ecuație pentru circumcercul în coordonate triliniare x  : y  : z este a / x + b / y + c / z = 0 . O ecuație pentru circumcercul în coordonate barentric x  : y  : z este a ² / x + b ² / y + c ² / z = 0 .

Izogonal conjugat al circumscris este linia de la infinit, dat în coordonate triliniare de ax + de + cz = 0 și în coordonate barycentric prin x + y + z = 0 .

Dimensiuni mai mari

În plus, circumcercul unui triunghi încorporat în dimensiuni d poate fi găsit folosind o metodă generalizată. Să A , B și C să fie d puncte -dimensionale, care formează vârfurile unui triunghi. Începem prin transpunerea sistemului pentru a plasa C la origine:

${\ displaystyle {\ begin {align} \ mathbf {a} & = \ mathbf {A} - \ mathbf {C}, \\\ mathbf {b} & = \ mathbf {B} - \ mathbf {C}. \ sfârșit {aliniat}}}$

Circumradiusul, r , este atunci

${\ displaystyle r = {\ frac {\ left \ | \ mathbf {a} \ right \ | \ left \ | \ mathbf {b} \ right \ | \ left \ | \ mathbf {a} - \ mathbf {b} \ right \ |} {2 \ left \ | \ mathbf {a} \ times \ mathbf {b} \ right \ |}} = {\ frac {\ left \ | \ mathbf {a} - \ mathbf {b} \ dreapta \ |} {2 \ sin \ theta}} = {\ frac {\ left \ | \ mathbf {A} - \ mathbf {B} \ right \ |} {2 \ sin \ theta}},}$

unde θ este unghiul interior dintre a și b . Circumcentrul, p ₀ , este dat de

${\ displaystyle p_ {0} = {\ frac {(\ left \ | \ mathbf {a} \ right \ | ^ {2} \ mathbf {b} - \ left \ | \ mathbf {b} \ right \ | ^ {2} \ mathbf {a}) \ times (\ mathbf {a} \ times \ mathbf {b})} {2 \ left \ | \ mathbf {a} \ times \ mathbf {b} \ right \ | ^ { 2}}} + \ mathbf {C}.}$

Această formulă funcționează numai în trei dimensiuni, deoarece produsul încrucișat nu este definit în alte dimensiuni, dar poate fi generalizat la celelalte dimensiuni prin înlocuirea produselor încrucișate cu următoarele identități:

${\ displaystyle {\ begin {align} (\ mathbf {a} \ times \ mathbf {b}) \ times \ mathbf {c} & = (\ mathbf {a} \ cdot \ mathbf {c}) \ mathbf {b } - (\ mathbf {b} \ cdot \ mathbf {c}) \ mathbf {a}, \\\ mathbf {a} \ times (\ mathbf {b} \ times \ mathbf {c}) & = (\ mathbf {a} \ cdot \ mathbf {c}) \ mathbf {b} - (\ mathbf {a} \ cdot \ mathbf {b}) \ mathbf {c}, \\\ left \ | \ mathbf {a} \ times \ mathbf {b} \ right \ | ^ {2} & = \ left \ | \ mathbf {a} \ right \ | ^ {2} \ left \ | \ mathbf {b} \ right \ | ^ {2} - (\ mathbf {a} \ cdot \ mathbf {b}) ^ {2}. \ end {align}}}$

Coordonatele circumcentrului

Coordonatele carteziene

De coordonatele carteziene ale circumscris sunt ${\ displaystyle U = \ left (U_ {x}, U_ {y} \ right)}$

${\ displaystyle {\ begin {align} U_ {x} & = {\ frac {1} {D}} \ left [(A_ {x} ^ {2} + A_ {y} ^ {2}) (B_ { y} -C_ {y}) + (B_ {x} ^ {2} + B_ {y} ^ {2}) (C_ {y} -A_ {y}) + (C_ {x} ^ {2} + C_ {y} ^ {2}) (A_ {y} -B_ {y}) \ right] \\ [5pt] U_ {y} & = {\ frac {1} {D}} \ left [(A_ { x} ^ {2} + A_ {y} ^ {2}) (C_ {x} -B_ {x}) + (B_ {x} ^ {2} + B_ {y} ^ {2}) (A_ { x} -C_ {x}) + (C_ {x} ^ {2} + C_ {y} ^ {2}) (B_ {x} -A_ {x}) \ right] \ end {align}}}$

cu

${\ displaystyle D = 2 \ left [A_ {x} (B_ {y} -C_ {y}) + B_ {x} (C_ {y} -A_ {y}) + C_ {x} (A_ {y} -B_ {y}) \ dreapta]. \,}$

Fără pierderea generalității, acest lucru poate fi exprimat într-o formă simplificată după traducerea vârfului A la originea sistemelor de coordonate carteziene, adică atunci când A ′ = A - A = ( A ′ _x , A ′ _y ) = (0, 0) . În acest caz, coordonatele vârfurilor B ′ = B - A și C ′ = C - A reprezintă vectorii de la vârful A ′ la acești vârfuri. Observați că această traducere banală este posibilă pentru toate triunghiurile și că circumcentrul triunghiului A ′ B ′ C ′ urmează ca ${\ displaystyle U '= (U' _ {x}, U '_ {y})}$

${\ displaystyle {\ begin {align} U '_ {x} & = {\ frac {1} {D'}} \ left [C '_ {y} ({B' _ {x}} ^ {2} + {B '_ {y}} ^ {2}) - B' _ {y} ({C '_ {x}} ^ {2} + {C' _ {y}} ^ {2}) \ right ], \\ [5pt] U '_ {y} & = {\ frac {1} {D'}} \ left [B '_ {x} ({C' _ {x}} ^ {2} + { C '_ {y}} ^ {2}) - C' _ {x} ({B '_ {x}} ^ {2} + {B' _ {y}} ^ {2}) \ right] \ sfârșit {aliniat}}}$

cu

${\ displaystyle D '= 2 (B' _ {x} C '_ {y} -B' _ {y} C '_ {x}). \,}$

Datorită translației vârfului A la origine, circumradius r poate fi calculat ca

${\ displaystyle r = \ | U '\ | = {\ sqrt {{U' _ {x}} ^ {2} + {U '_ {y}} ^ {2}}}}$

iar circumcentrul propriu-zis al ABC urmează după cum

${\ displaystyle U = U '+ A}$

Coordonate triliniare

Circumcentrul are coordonate triliniare

cos α  : cos β  : cos γ

unde α , β , γ sunt unghiurile triunghiului.

În ceea ce privește lungimile laterale a, b, c , triliniarele sunt

${\ displaystyle a \ left (b ^ {2} + c ^ {2} -a ^ {2} \ right): b \ left (c ^ {2} + a ^ {2} -b ^ {2} \ dreapta): c \ left (a ^ {2} + b ^ {2} -c ^ {2} \ dreapta).}$

Coordonatele baricentrice

Circumcentrul are coordonate barycentric

${\ displaystyle a ^ {2} \ left (b ^ {2} + c ^ {2} -a ^ {2} \ right): \; b ^ {2} \ left (c ^ {2} + a ^ {2} -b ^ {2} \ right): \; c ^ {2} \ left (a ^ {2} + b ^ {2} -c ^ {2} \ right), \,}$

unde a , b , c sunt lungimi de margine ( BC , CA , respectiv AB ) ale triunghiului.

În ceea ce privește unghiurile triunghiului, coordonatele baricentrice ale circumcentrului sunt ${\ displaystyle \ alpha, \ beta, \ gamma,}$

${\ displaystyle \ sin 2 \ alpha: \ sin 2 \ beta: \ sin 2 \ gamma.}$

Vector circumcentr

Deoarece coordonatele carteziene ale oricărui punct sunt o medie ponderată a celor ale vârfurilor, greutățile fiind coordonatele barcentric ale punctului normalizate pentru a însuma la unitate, vectorul circumcentric poate fi scris ca

${\ displaystyle U = {\ frac {a ^ {2} \ left (b ^ {2} + c ^ {2} -a ^ {2} \ right) A + b ^ {2} \ left (c ^ { 2} + a ^ {2} -b ^ {2} \ right) B + c ^ {2} \ left (a ^ {2} + b ^ {2} -c ^ {2} \ right) C} { a ^ {2} \ left (b ^ {2} + c ^ {2} -a ^ {2} \ right) + b ^ {2} \ left (c ^ {2} + a ^ {2} -b ^ {2} \ right) + c ^ {2} \ left (a ^ {2} + b ^ {2} -c ^ {2} \ right)}}.}$

Aici U este vectorul circumcentrului și A, B, C sunt vectorii de vârf. Divizorul de aici este egal cu 16 S ² unde S este aria triunghiului. După cum sa menționat anterior

${\ displaystyle {\ begin {align} \ mathbf {a} & = \ mathbf {A} - \ mathbf {C}, \\\ mathbf {b} & = \ mathbf {B} - \ mathbf {C}. \ sfârșit {aliniat}}}$

Coordonatele carteziene din produsele încrucișate și puncte

În spațiul euclidian , există un cerc unic care trece prin oricare trei puncte necoliniare date P ₁ , P ₂ și P ₃ . Folosind coordonatele carteziene pentru a reprezenta aceste puncte ca vectori spațiali , este posibil să se utilizeze produsul punct și produsul încrucișat pentru a calcula raza și centrul cercului. Lăsa

${\ displaystyle \ mathrm {P_ {1}} = {\ begin {bmatrix} x_ {1} \\ y_ {1} \\ z_ {1} \ end {bmatrix}}, \ mathrm {P_ {2}} = {\ begin {bmatrix} x_ {2} \\ y_ {2} \\ z_ {2} \ end {bmatrix}}, \ mathrm {P_ {3}} = {\ begin {bmatrix} x_ {3} \\ y_ {3} \\ z_ {3} \ end {bmatrix}}}$

Apoi raza cercului este dată de

${\ displaystyle \ mathrm {r} = {\ frac {\ left | P_ {1} -P_ {2} \ right | \ left | P_ {2} -P_ {3} \ right | \ left | P_ {3} -P_ {1} \ right |} {2 \ left | \ left (P_ {1} -P_ {2} \ right) \ times \ left (P_ {2} -P_ {3} \ right) \ right |} }}$

Centrul cercului este dat de combinația liniară

${\ displaystyle \ mathrm {P_ {c}} = \ alpha \, P_ {1} + \ beta \, P_ {2} + \ gamma \, P_ {3}}$

Unde

${\ displaystyle {\ begin {align} \ alpha = {\ frac {\ left | P_ {2} -P_ {3} \ right | ^ {2} \ left (P_ {1} -P_ {2} \ right) \ cdot \ left (P_ {1} -P_ {3} \ right)} {2 \ left | \ left (P_ {1} -P_ {2} \ right) \ times \ left (P_ {2} -P_ { 3} \ right) \ right | ^ {2}}} \\\ beta = {\ frac {\ left | P_ {1} -P_ {3} \ right | ^ {2} \ left (P_ {2} - P_ {1} \ right) \ cdot \ left (P_ {2} -P_ {3} \ right)} {2 \ left | \ left (P_ {1} -P_ {2} \ right) \ times \ left ( P_ {2} -P_ {3} \ right) \ right | ^ {2}}} \\\ gamma = {\ frac {\ left | P_ {1} -P_ {2} \ right | ^ {2} \ left (P_ {3} -P_ {1} \ right) \ cdot \ left (P_ {3} -P_ {2} \ right)} {2 \ left | \ left (P_ {1} -P_ {2} \ dreapta) \ times \ left (P_ {2} -P_ {3} \ right) \ right | ^ {2}}} \ end {align}}}$

Locație relativ la triunghi

Poziția circumcentrului depinde de tipul de triunghi:

• Pentru un triunghi acut (toate unghiurile mai mici decât un unghi drept), circumcentrul se află întotdeauna în interiorul triunghiului.
• Pentru un triunghi dreptunghiular, circumcentrul se află întotdeauna în punctul mijlociu al hipotenuzei . Aceasta este o formă a teoremei lui Thales .
• Pentru un triunghi obtuz (un triunghi cu un unghi mai mare decât un unghi drept), circumcentrul se află întotdeauna în afara triunghiului.

Aceste caracteristici de localizare pot fi văzute luând în considerare coordonatele triliniare sau barientrice date mai sus pentru circumcentr: toate cele trei coordonate sunt pozitive pentru orice punct interior, cel puțin o coordonată este negativă pentru orice punct exterior și o coordonată este zero și două sunt pozitive pentru un punct non-vertex pe o latură a triunghiului.

Unghiuri

Unghiurile pe care cercul circumscris le formează cu laturile triunghiului coincid cu unghiurile la care laturile se întâlnesc. Unghiul lateral opus α întâlnește cercul de două ori: o dată la fiecare capăt; în fiecare caz la unghiul α (în mod similar pentru celelalte două unghiuri). Acest lucru se datorează teoremei segmentului alternativ , care afirmă că unghiul dintre tangentă și coardă este egal cu unghiul din segmentul alternativ.

Triunghiul se concentrează pe circumcercul triunghiului ABC

În această secțiune, unghiurile de vârf sunt etichetate A , B , C și toate coordonatele sunt coordonate triliniare :

• Punctul Steiner = bc / ( b ² - c ² ): ca / ( c ² - a ² ): ab / ( a ² - b ² ) = punctul nonvertex de intersecție al circumcercului cu elipsa Steiner. ( Elipsa Steiner , cu centru = centroid ( ABC ), este elipsa celei mai mici zone care trece prin A , B și C. O ecuație pentru această elipsă este 1 / ( ax ) + 1 / ( cu ) + 1 / ( cz ) = 0. )
• Tarry point = sec ( A + ω): sec ( B + ω): sec ( C + ω) = antipod al punctului Steiner
• Focusul parabolei Kiepert = csc ( B - C ): csc ( C - A ): csc ( A - B ).

Alte proprietăți

Diametrul de circumscris, numit circumdiameter și egală cu dublul circumscris , poate fi calculat ca lungimea oricărei laturi a triunghiului împărțit la sinusul a opus unghiului :

${\ displaystyle {\ text {diametru}} = {\ frac {a} {\ sin A}} = {\ frac {b} {\ sin B}} = {\ frac {c} {\ sin C}}. }$

Ca o consecință a legii sinelor , nu contează ce parte și unghi opus sunt luate: rezultatul va fi același.

Diametrul circumcercului poate fi exprimat și ca

${\ displaystyle {\ begin {align} {\ text {diametru}} & {} = {\ frac {abc} {2 \ cdot {\ text {area}}}} = {\ frac {| AB || BC | | CA |} {2 | \ Delta ABC |}} \\ [5pt] & {} = {\ frac {abc} {2 {\ sqrt {s (sa) (sb) (sc)}}}} \\ [5pt] & {} = {\ frac {2abc} {\ sqrt {(a + b + c) (- a + b + c) (a-b + c) (a + bc)}}} \ end { aliniat}}}$

unde a , b , c sunt lungimile laturilor triunghiului și s = ( a + b + c ) / 2 este semiperimetrul. Expresia de mai sus este aria triunghiului, după formula lui Heron . Expresiile trigonometrice pentru diametrul circumcercului includ ${\ displaystyle {\ sqrt {\ scriptstyle {s (sa) (sb) (sc)}}}}$

${\ displaystyle {\ text {diametru}} = {\ sqrt {\ frac {2 \ cdot {\ text {area}}} {\ sin A \ sin B \ sin C}}}.}$

Cercul de nouă puncte al triunghiului are jumătate din diametrul circumcercului.

În orice triunghi dat, circumcentrul este întotdeauna coliniar cu centroidul și ortocentrul . Linia care trece prin toate acestea este cunoscută sub numele de linia Euler .

Izogonal conjugat al circumscris este orthocenter .

Cercul de limitare minim util de trei puncte este definit fie de circumcerc (unde trei puncte sunt pe cercul de limitare minim), fie de cele două puncte ale celei mai lungi laturi a triunghiului (unde cele două puncte definesc un diametru al cercului). Este obișnuit să se confunde cercul minim de limitare cu cercul circular.

Circumscrierea a trei puncte coliniare este linia pe care se află cele trei puncte, denumită adesea un cerc cu rază infinită . Punctele aproape coliniare duc adesea la instabilitate numerică în calculul circumcercului.

Cercurile de triunghiuri au o relație intimă cu triangulația Delaunay a unui set de puncte.

Prin teorema lui Euler în geometrie , distanța dintre circumcentrul O și incinerul I este

${\ displaystyle OI = {\ sqrt {R (R-2r)}},}$

unde r este raza de cerc și R este raza de circumcerc ; prin urmare circumradius este cel puțin de două ori inradius ( inegalitatea triunghiului lui Euler ), cu egalitate numai în cazul echilateral .

Distanța dintre O și ortocentrul H este

${\ displaystyle OH = {\ sqrt {R ^ {2} -8R ^ {2} \ cos A \ cos B \ cos C}} = {\ sqrt {9R ^ {2} - (a ^ {2} + b ^ {2} + c ^ {2})}}.}$

Pentru centroidul G și centrul cu nouă puncte N avem

${\ displaystyle {\ begin {align} IG & <IO, \\ 2IN & <IO, \\ OI ^ {2} & = 2R \ cdot IN. \ end {align}}}$

Produsul razei de cerc și a razei de circumcerc a unui triunghi cu laturile a , b și c este

${\ displaystyle rR = {\ frac {abc} {2 (a + b + c)}}.}$

Cu circumradius R , laturile a , b , c și medianele m _a , m _b și m _c , avem

${\ displaystyle {\ begin {align} 3 {\ sqrt {3}} R & \ geq a + b + c \\ [5pt] 9R ^ {2} & \ geq a ^ {2} + b ^ {2} + c ^ {2} \\ [5pt] {\ frac {27} {4}} R ^ {2} & \ geq m_ {a} ^ {2} + m_ {b} ^ {2} + m_ {c} ^ {2}. \ End {align}}}$

Dacă mediană m , altitudinea h , și bisectoarea intern t toate emană de la același vârful unui triunghi cu circumscris R , atunci

${\ displaystyle 4R ^ {2} h ^ {2} (t ^ {2} -h ^ {2}) = t ^ {4} (m ^ {2} -h ^ {2}).}$

Teorema lui Carnot afirmă că suma distanțelor de la circumcenter la cele trei laturi este egală cu suma circumradiusului și a inradiusului . Aici lungimea unui segment este considerată a fi negativă dacă și numai dacă segmentul se află în întregime în afara triunghiului.

Dacă un triunghi are două cercuri particulare ca circumcerc și circumferință , există un număr infinit de alte triunghiuri cu același circumferință și circumferință, cu orice punct de pe circumferință ca vârf. (Acesta este cazul n  = 3 al porismului lui Poncelet ). O condiție necesară și suficientă pentru ca astfel de triunghiuri să existe este egalitatea de mai sus${\ displaystyle OI = {\ sqrt {R (R-2r)}}.}$

Cadrilatere ciclice

Cadrilaterele care pot fi circumscrise au proprietăți particulare, inclusiv faptul că unghiurile opuse sunt unghiuri suplimentare (adunând până la 180 ° sau π radiani).

N -gone ciclice

Pentru un poligon ciclic cu un număr impar de laturi, toate unghiurile sunt egale dacă și numai dacă poligonul este regulat. Un poligon ciclic cu un număr par de laturi are toate unghiurile egale dacă și numai dacă laturile alternative sunt egale (adică laturile 1, 3, 5, ... sunt egale, iar laturile 2, 4, 6, ... sunt egale).

Un pentagon ciclic cu laturi și suprafețe raționale este cunoscut sub numele de pentagon Robbins ; în toate cazurile cunoscute, diagonalele sale au și lungimi raționale.

În orice n -gon ciclic cu n , suma unui set de unghiuri alternative (primul, al treilea, al cincilea etc.) este egală cu suma celuilalt set de unghiuri alternative. Acest lucru poate fi dovedit prin inducția din cazul n = 4, în fiecare caz înlocuind o latură cu încă trei laturi și observând că aceste trei laturi noi împreună cu latura veche formează un patrulater care are ea însăși această proprietate; unghiurile alternative ale celui din urmă patrulater reprezintă adaosurile la sumele unghiulare alternative ale n -gonului anterior .

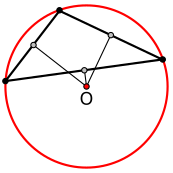
Să fie înscris un n -gon într-un cerc și să fie un alt n -gon tangențial acelui cerc la vârfurile primului n -gon. Apoi, din orice punct P de pe cerc, produsul distanțelor perpendiculare de la P la laturile primului n -gon este egal cu produsul distanțelor perpendiculare de la P la laturile celui de-al doilea n -gon.

Punctul pe circumcerc

Fie un n -gon ciclic să aibă vârfuri A ₁ , ..., A _n pe cercul unității. Apoi, pentru orice punct M de pe arcul minor A ₁ A _n , distanțele de la M la vârfuri sunt satisfăcute

${\ displaystyle {\ begin {cases} MA_ {1} + MA_ {3} + \ cdots + MA_ {n-2} + MA_ {n} <n / {\ sqrt {2}} și {\ text {if} } n {\ text {este impar}}; \\ MA_ {1} + MA_ {3} + \ cdots + MA_ {n-3} + MA_ {n-1} \ leq n / {\ sqrt {2}} & {\ text {if}} n {\ text {este chiar}}. \ end {cases}}}$

Pentru un n -gon regulat , dacă sunt distanțele de la orice punct al circumcercului la vârfuri , atunci ${\ displaystyle MA_ {i}}$${\ displaystyle M}$${\ displaystyle A_ {i}}$

${\ displaystyle 3 (MA_ {1} ^ {2} + MA_ {2} ^ {2} + ... + MA_ {n} ^ {2}) ^ {2} = 2n (MA_ {1} ^ {4 } + MA_ {2} ^ {4} + ... + MA_ {n} ^ {4}).}$

Constanta de circumscriere a poligonului

Orice poligon regulat este ciclic. Luați în considerare un cerc unitar, apoi circumscrieți un triunghi regulat astfel încât fiecare parte să atingă cercul. Circumscrie un cerc, apoi circumscrie un pătrat. Circumscrie din nou un cerc, apoi circumscrie un pentagon regulat și așa mai departe. Razele cercurilor circumscrise converg către așa-numita constantă de circumscriere a poligonului

${\ displaystyle \ prod _ {n = 3} ^ {\ infty} {\ frac {1} {\ cos \ left ({\ frac {\ pi} {n}} \ right)}} = 8.7000366 \ ldots.}$

(secvența A051762 în OEIS ). Reciprocul acestei constante este constanta Kepler – Bouwkamp .

Vezi si

• Circumcentrul de masă
• Circumgon
• Sferă circumscrisă
• Cerc inscris
• Teorema japoneză pentru poligoane ciclice
• Teorema japoneză pentru patrulaterele ciclice
• Teorema lui Jung , o inegalitate care leagă diametrul unui punct stabilit de raza sferei sale limită minime
• Teorema Kosniței
• Teorema lui Lester
• Poligon tangențial
• Centrul triunghiului

Referințe

linkuri externe

• Derivarea formulei pentru raza circumcercului de triunghi la Mathalino.com
• Gons-unghiuri și gons-uri semi-regulate: generalizări respective ale dreptunghiurilor și rombilor la Schițe de geometrie dinamică, schiță de geometrie dinamică interactivă.

MathWorld

• Weisstein, Eric W. „Circumcircle” . MathWorld .
• Weisstein, Eric W. „Poligon ciclic” . MathWorld .
• Weisstein, Eric W. „Steiner circumellipse” . MathWorld .

Interactiv

• Triunghi circumcerc și circumcentru Cu animație interactivă
• Un applet Java interactiv pentru circumcenter