Configurare vertex - Vertex configuration

Icosidodecahedron.png
Icosidodecaedru 		Icosidodecaedru vertfig etichetat.png
Figura de
vârf reprezentată ca 3.5.3.5 sau (3.5) 2

În geometrie , o configurație de vârf este o notație de scurtătură pentru reprezentarea figurii de vârf a unui poliedru sau a plăcilor ca secvența fețelor din jurul unui vârf. Pentru poliedre uniforme există un singur tip de vârf și, prin urmare, configurația vârfului definește pe deplin poliedrul. ( Poliedrele chirale există în perechi oglindă-imagine cu aceeași configurație de vârf.)

O configurație de vârf este dată ca o succesiune de numere reprezentând numărul de laturi ale fețelor care înconjoară vârful. Notația „ ABC “ descrie un nod care are 3 fețe în jurul ei, se confruntă cu o , b , și c părți.

De exemplu, „3.5.3.5” indică un vârf aparținând a 4 fețe, alternând triunghiuri și pentagone . Această configurație de vârf definește icosidodecaedrul tranzitiv al vârfului . Notația este ciclică și, prin urmare, este echivalentă cu puncte de plecare diferite, deci 3.5.3.5 este același cu 5.3.5.3. Ordinea este importantă, deci 3.3.5.5 este diferită de 3.5.3.5. (Primul are două triunghiuri urmate de două pentagone.) Elementele repetate pot fi colectate ca exponenți, astfel încât acest exemplu este reprezentat și ca (3.5) 2 .

Acesta a fost numit în mod variat o descriere vertex , tip vertex , simbolul vertex , aranjamentul vertex , model vertex , fata-vector . Este, de asemenea, numit simbol Cundy și Rollett pentru utilizarea sa pentru solidele arhimede în cartea lor din 1952 Modele matematice .

Cifre de vârf

O configurație de vârf poate fi, de asemenea, reprezentată ca o figură de vârf poligonală care arată fețele din jurul vârfului. Această figură de vârf are o structură tridimensională, deoarece fețele nu sunt în același plan pentru poliedre, dar pentru poliedrele uniforme la vârf, toate vârfurile vecine sunt în același plan și astfel această proiecție a planului poate fi utilizată pentru a reprezenta vizual configurația vârfului .

Variații și utilizări

Plase de cifre cu vârf regulat, { p , q } = p q
Polyiamond-3-1.svg
{3,3} = 3 3
Defect 180 ° 		Polyiamond-4-1.svg
{3,4} = 3 4
Defect 120 ° 		Polyiamond-5-4.svg
{3,5} = 3 5
Defect 60 ° 		Polyiamond-6-11.svg
{3,6} =

3 6
Defect 0 °

TrominoV.jpg
{4,3}
Defect la 90 ° 		Tiglă pătrată vertfig.png
{4,4} =

4 4
Defect 0 °

Pentagon net.png
{5,3} = 5 3
Defect 36 ° 		Tiglă hexagonală vertfig.png
{6,3} =

6 3
Defect 0 °

Un vârf are nevoie de cel puțin 3 fețe și un defect unghiular .
Un defect al unghiului de 0 ° va umple planul euclidian cu o placare obișnuită.
Prin teorema lui Descartes , numărul vârfurilor este de 720 ° / defect (4π radiani / defect ).

Se folosesc notații diferite, uneori cu separator de virgulă (,) și alteori punct (.). Operatorul de perioadă este util, deoarece arată ca un produs și poate fi utilizată o notație exponentă. De exemplu, 3.5.3.5 este uneori scris ca (3.5) 2 .

Notarea poate fi, de asemenea, considerată o formă expansivă a simbolului simplu Schläfli pentru poliedre regulate . Notația Schläfli { p , q } înseamnă q p -gone în jurul fiecărui vârf. Deci { p , q } poate fi scris ca ppp .. ( q ori) sau p q . De exemplu, un icosaedru este {3,5} = 3.3.3.3.3 sau 3 5 .

Această notație se aplică învelișurilor poligonale, precum și poliedrelor. O configurație de vârf planar denotă o placare uniformă la fel ca o configurație de vârf nonplană denotă un poliedru uniform.

Notarea este ambiguă pentru formele chirale . De exemplu, cubul snub are forme în sensul acelor de ceasornic și în sens invers acelor de ceasornic, care sunt identice în imaginile oglindă. Ambele au o configurație de vârf 3.3.3.3.4.

Poligoane stelare

Notația se aplică și pentru fețele regulate neconvexe, poligoanele stelare . De exemplu, o pentagramă are simbolul {5/2}, adică are 5 laturi care înconjoară centrul de două ori.

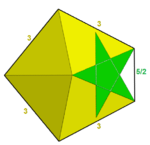
De exemplu, există 4 poliedre stelare regulate cu poligon regulat sau figuri de vârf poligon stelare. Mici Dodecaedrul stelat are simbolul Schläfli de {5 / 2,5} care se extinde într - o configurație vertex explicit 5 / 2,5 / 2,5 / 2,5 / 2,5 / 2 sau combinate ca (5/2) 5 . Mare Dodecaedrul stelat , {5 / 2,3} are o figură triunghiulară vertex și configurație (5 / 2,5 / 2,5 / 2) sau (5/2) 3 . Mare dodecaedron , {5,5 / 2} are o cifră vertex pentagrammic, cu configurația vertex este (5.5.5.5.5) / 2 sau (5 5 ) / 2. Un mare icosaedru , {3,5 / 2} are, de asemenea, o figură de vârf pentagrammic, cu configurație de vârf (3.3.3.3.3) / 2 sau (3 5 ) / 2.

Dodecaedru mic stelat vertfig.png Mare dodecaedru stelat vertfig.png Great snub icosidodecahedron vertfig.png Mare retrosnub icosidodecaedru vertfig.png Micul retrosnub icosicosidodecaedru vertfig.png
{5 / 2,5} = (5/2) 5 {5 / 2,3} = (5/2) 3 3 4 .5 / 2 3 4 .5 / 3 (3 4 .5 / 2) / 2
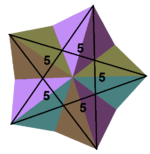
Mare dodecaedru vertfig.png Mare icosaedru vertfig.svg DU57 facets.png DU72 facets.png DU74 facets.png
{5,5 / 2} = (5 5 ) / 2 {3,5 / 2} = (3 5 ) / 2 V.3 4 .5 / 2 V3 4 .5 / 3 V (3 4 .5 / 2) / 2

Poligoane inversate

Se consideră că fețele de pe o figură de vârf progresează într-o singură direcție. Unele poliedre uniforme au figuri de vârf cu inversiuni în care fețele progresează retrograd. O figură de vârf reprezintă acest lucru în notația poligonului stelelor laturilor p / q astfel încât p <2 q , unde p este numărul de laturi și q numărul de spire în jurul unui cerc. De exemplu, „3/2” înseamnă un triunghi care are vârfuri care se învârt de două ori, care este la fel ca o dată înapoi. În mod similar, „5/3” este o pentagramă înapoi 5/2.

Toate configurațiile de vârf uniforme ale poligoanelor convexe regulate

A se vedea, de asemenea: Archimedean_solid § Clasificare , Tiglă prin poligoane regulate § Combinații de poligoane regulate care se pot întâlni la un vârf și Tiglă uniformă § Liste extinse de plăci uniforme

Poliedrele semiregulare au configurații de vârf cu defect unghiular pozitiv .

NOTĂ: Figura de vârf poate reprezenta o placare regulată sau semiregulară pe plan dacă defectul său este zero. Poate reprezenta o placare a planului hiperbolic dacă defectul său este negativ.

Pentru poliedre uniforme, defectul unghiului poate fi utilizat pentru a calcula numărul de vârfuri. Teorema lui Descartes afirmă că toate defectele unghiulare într-o sferă topologică trebuie să însumeze 4 π  radiani sau 720 grade.

Deoarece poliedrele uniforme au toate vârfurile identice, această relație ne permite să calculăm numărul de vârfuri, care este 4 π / defect sau 720 / defect .

Exemplu: Un cub trunchiat 3.8.8 are un defect unghiular de 30 de grade. Prin urmare, are 720/30 = 24 vârfuri.

În special rezultă că { a , b } are 4 / (2 - b (1 - 2 / a )) vârfuri.

Fiecare configurație de vârf enumerată potențial definește în mod unic un poliedru semiregular. Cu toate acestea, nu toate configurațiile sunt posibile.

Cerințele topologice limitează existența. În mod specific pqr implică faptul că un p -gon este înconjurat de q -goni alternativi și r -goni, deci fie p este egal, fie q este egal cu r . În mod similar, q este egal sau p este egal cu r , iar r este egal sau p este egal cu q . Prin urmare, triplele potențial posibile sunt 3.3.3, 3.4.4, 3.6.6, 3.8.8, 3.10.10, 3.12.12, 4.4. n (pentru orice n > 2), 4.6.6, 4.6.8, 4.6.10, 4.6.12, 4.8.8, 5.5.5, 5.6.6, 6.6.6. De fapt, toate aceste configurații cu trei fețe întâlnite la fiecare vârf se dovedesc a exista.

Numărul dintre paranteze este numărul de vârfuri, determinat de defectul unghiului.

Tripluri
Cvadrupluri
Cvintupluri
Sextuple

Configurarea feței

Dodecaedru rombic

Solidele duale sau catalane uniforme , inclusiv bipiramidele și trapezohedra , sunt vertical-regulate ( față-tranzitive ) și astfel pot fi identificate printr-o notație similară care este uneori numită configurație a feței . Cundy și Rollett prefixată aceste simboluri duale de un V . În contrast, Plăcile și modelele utilizează paranteze pătrate în jurul simbolului pentru plăcile izoedrice.

Această notație reprezintă un număr secvențial al numărului de fețe care există la fiecare vârf în jurul unei fețe . De exemplu, V3.4.3.4 sau V (3.4) 2 reprezintă dodecaedrul rombic care este tranzitiv față: fiecare față este un romb , iar vârfurile alternante ale rombului conțin 3 sau 4 fețe fiecare.

Note

Referințe

  • Cundy, H. și Rollett, A., Mathematical Models (1952), (ediția a III-a, 1989, Stradbroke, Anglia: Tarquin Pub.), 3.7 The Archimedean Polyhedra . Pp. 101–115, pp. 118–119 Tabelul I, Plasele dualilor arhimedici, V. a . b . c ... ca simboluri regulate-verticale .
  • Peter Cromwell, Polyhedra , Cambridge University Press (1977) The Archimedean solid. Pp. 156–167.
  • Williams, Robert (1979). Fundația geometrică a structurii naturale: o carte sursă de proiectare . Dover Publications, Inc. ISBN   0-486-23729-X . Folosește simbolul Cundy-Rollett.
  • Grünbaum, Branko ; Shephard, GC (1987). Placaje și modele . WH Freeman and Company. ISBN   0-7167-1193-1 . Pp. 58–64, Plăcile de poligoane regulate abc ... (Tiglele prin poligoane regulate și poligoane stelare) pp. 95–97, 176, 283, 614–620, Simbolul de placare monoedrică [v 1 .v 2 . ... .v r ]. pp. 632–642 plăci goale.
  • The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN   978-1-56881-220-5 (p. 289 Cifre Vertex, folosește separatorul de virgule, pentru solidele și plăcile arhimedeice).

linkuri externe