Fagure cubice - Cubic honeycomb

Fagure cubic

Tip	Fagure regulat
Familie	Fagure de hipercub
Indexare	J _11,15 , A ₁ W ₁ , G ₂₂
Simbolul Schläfli	{4,3,4}
Diagrama Coxeter
Tipul celulei	{4,3}
Tipul feței	pătrat {4}
Figura Vertex	octaedru
Notare Fibrifold din grupul spațial	Pm 3 m (221) 4 ^- : 2
Grupul Coxeter	${\ displaystyle {\ tilde {C}} _ {3}}$ , [4,3,4]
Dual	celula auto-duala :
Proprietăți	Vertex-tranzitiv , regulat

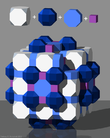
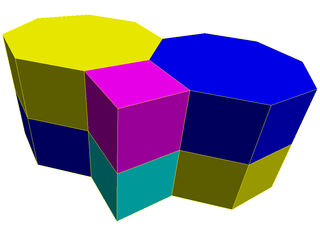
Fagure cubic sau cellulation cubic este singura adecvată regulată spațiu de umplere tessellation (sau fagure ) în Euclidian 3-space , format din cubi celule. Are 4 cuburi în jurul fiecărei margini și 8 cuburi în jurul fiecărui vârf. Figura sa de vârf este un octaedru regulat . Este o teselare auto-duală cu simbolul Schläfli {4,3,4}. John Horton Conway numește acest fagure de cubilă .

Un fagure geometric este o umplere a spațiului de celule poliedrice sau cu dimensiuni superioare , astfel încât să nu existe goluri. Este un exemplu al plăcilor matematice sau teselelor mai generale în orice număr de dimensiuni.

Fagurii sunt de obicei construiți în spațiul euclidian obișnuit („plat”), ca fagurii uniformi conveși . Ele pot fi, de asemenea, construite în spații neeuclidiene , cum ar fi fagurii uniformi hiperbolici . Orice politop uniform finit poate fi proiectat în circumfera sa pentru a forma un fagure uniform în spațiul sferic.

Faguri înrudiți

Face parte dintr-o familie multidimensională de faguri de hipercub , cu simboluri Schläfli de forma {4,3, ..., 3,4}, începând cu placarea pătrată , {4,4} în plan.

Este unul dintre cei 28 de faguri uniformi care folosesc celule poliedrice uniforme convexe .

Izometriile rețelelor cubice simple

Rețelele cubice simple pot fi distorsionate în simetrii inferioare, reprezentate de sisteme de cristale inferioare:

Sistem de cristal	Triclinica monoclinică	Orthorhombic	Tetragonal	Romboedric	Cub
Celula unitară	Paralelipiped	Cuboid dreptunghiular	Cuboid pătrat	Trapezohedron trigonal	cub
Grup de puncte Subgrupul Rotire ordine	[], (*) Comanda 2 [] ⁺ , (1)	[2,2], (* 222) Ordinul 8 [2,2] ⁺ , (222)	[4,2], (* 422) Ordinul 16 [4,2] ⁺ , (422)	[3], (* 33) Ordinul 6 [3] ⁺ , (33)	[4,3], (* 432) Ordinul 48 [4,3] ⁺ , (432)
Diagramă
Subgrupul de rotație al grupului spațial	Pm (6) P1 (1)	Pmmm (47) P222 (16)	P4 / mmm (123) P422 (89)	R3m (160) R3 (146)	Pm 3 m (221) P432 (207)
Notare Coxeter	-	[∞] _a × [∞] _b × [∞] _c	[4,4] _a × [∞] _c	-	[4,3,4] _a
Diagrama Coxeter	-			-

Coloranți uniformi

Există un număr mare de coloranți uniformi , derivați din diferite simetrii. Acestea includ:

Notare Coxeter Grup spațial	Diagrama Coxeter	Simbolul Schläfli	Culori după litere
[4,3,4] Pm 3 m (221)	=	{4,3,4}	1: aaaa / aaaa
[4,3 ^1,1 ] = [4,3,4,1 ⁺ ] Fm 3 m (225)	=	{4,3 ^1,1 }	2: abba / baab
[4,3,4] Pm 3 m (221)		t _0,3 {4,3,4}	4: abbc / bccd
[[4,3,4]] Pm 3 m (229)		t _0,3 {4,3,4}	4: egumen / bbba
[4,3,4,2, ∞]	sau	{4,4} × t {∞}	2: aaaa / bbbb
[4,3,4,2, ∞]		t ₁ {4,4} × {∞}	2: abba / abba
[∞, 2, ∞, 2, ∞]		t {∞} × t {∞} × {∞}	4: abcd / abcd
[∞, 2, ∞, 2, ∞] = [4, (3,4) ^* ]	=	t {∞} × t {∞} × t {∞}	8: abcd / efgh

Proiecții

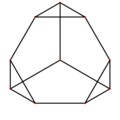
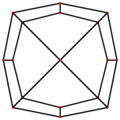
Fagure cubi poate fi proiectat ortogonal în planul euclidiană cu diferite aranjamente de simetrie. Cea mai mare simetrie (hexagonală) se proiectează într-o placă triunghiulară . O proiecție de simetrie pătrată formează o faianță pătrată .

Proiecții ortogonale
Simetrie	p6m (* 632)	p4m (* 442)	pmm (* 2222)
Solid
Cadru

Politopi și faguri asociați

Este legat de regulate 4-polytope Tesseract , simbolul Schläfli {4,3,3}, care există în 4-spațiu, și are doar 3 cuburi în jurul fiecare margine. Este, de asemenea, legat de fagurele cubic de ordinul 5 , simbolul Schläfli {4,3,5}, al spațiului hiperbolic cu 5 cuburi în jurul fiecărei margini.

Este într-o secvență de policoră și fagure de miere cu figuri de vârf octaedric .

{p, 3,4} faguri obișnuiți
Spaţiu	S ³	E ³	H ³
Formă	Finit	Afin	Compact	Paracompact	Noncompact
Nume	{3,3,4}	{4,3,4}	{5,3,4}	{6,3,4}	{7,3,4}	{8,3,4}	... {∞, 3,4}
Imagine
Celulele	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞, 3}

Este într-o secvență de politopi obișnuiți și faguri cu celule cubice .

{4,3, p} faguri obișnuiți
Spaţiu	S ³	E ³	H ³
Formă	Finit	Afin	Compact	Paracompact	Noncompact
Nume	{4,3,3}	{4,3,4}	{4,3,5}	{4,3,6}	{4,3,7}	{4,3,8}	... {4,3, ∞}
Imagine
Figura Vertex	{3,3}	{3,4}	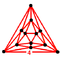{3,5}	{3,6}	{3,7}	{3,8}	{3, ∞}

{p, 3, p} faguri obișnuiți
Spaţiu	S ³	Euclidian E ³	H ³
Formă	Finit	Afin	Compact	Paracompact	Noncompact
Nume	{3,3,3}	{4,3,4}	{5,3,5}	{6,3,6}	{7,3,7}	{8,3,8}	... {∞, 3, ∞}
Imagine
Celulele	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞, 3}
Figura Vertex	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3, ∞}

Politopi înrudiți

Fagurele cubic are o simetrie mai mică ca fagure cubic runcinat, cu două dimensiuni de cuburi . O construcție dublă de simetrie poate fi construită prin plasarea unui cub mic în fiecare cub mare, rezultând un fagure neuniform cu cuburi , prisme pătrate și trapezoprisme dreptunghiulare (un cub cu simetrie D _2d ). Figura sa de vârf este o piramidă triunghiulară cu fețele sale laterale mărite de tetraedre.

Dual cell

Fagurele rezultate pot fi alternate pentru a produce un alt fagure neuniform cu tetraedre regulate , două tipuri de defenoide tetragonale, piramide triunghiulare și sfenoide. Figura sa de vârf are simetrie C _3v și are 26 de fețe triunghiulare, 39 de margini și 15 vârfuri.

Teselări euclidiene înrudite

[4,3,4], , Grupul Coxeter generează 15 permutări de teselări uniforme, 9 cu geometrie distinctă, inclusiv fagurele cubic alternat. Expandat fagure cubic ( de asemenea , cunoscut sub numele de fagure cubic runcinated) este identic cu geometrically fagure cubi.

Fagurii C3
Grup spațial	Fibrifold	Simetrie extinsă	Diagrama extinsă	Ordin	Fagurii
Pm 3 m (221)	4 ^- : 2	[4,3,4]		× 1	₁ , ₂ , ₃ , ₄ , ₅ , ₆
Fm 3 m (225)	2 ^- : 2	[1 ⁺ , 4,3,4] ↔ [4,3 ^1,1 ]	↔	Jumătate	₇ , ₁₁ , ₁₂ , ₁₃
I 4 3m (217)	4 ^o : 2	[[(4,3,4,2 ⁺ )]]		Jumătate × 2	₍₇₎ ,
Fd 3 m (227)	2 ⁺ : 2	[[1 ⁺ , 4,3,4,1 ⁺ ]] ↔ [[3 ^[4] ]]	↔	Trimestrul × 2	₁₀ ,
Im 3 m (229)	8 ^o : 2	[[4,3,4]]		× 2	₍₁₎ , ₈ , ₉

[4,3 ^1,1 ],, Grupul Coxeter generează 9 permutații de teselări uniforme, 4 cu geometrie distinctă, inclusiv fagurele cubic alternat.

Fagurii B3
Grup spațial	Fibrifold	Simetrie extinsă	Diagrama extinsă	Ordin	Fagurii
Fm 3 m (225)	2 ^- : 2	[4,3 ^1,1 ] ↔ [4,3,4,1 ⁺ ]	↔	× 1	₁ , ₂ , ₃ , ₄
Fm 3 m (225)	2 ^- : 2	<[1 ⁺ , 4,3 ^1,1 ]> ↔ <[3 ^[4] ]>	↔	× 2	₍₁₎ , ₍₃₎
Pm 3 m (221)	4 ^- : 2	<[4,3 ^1,1 ]>		× 2	₅ , ₆ , ₇ , ₍₆₎ , ₉ , ₁₀ , ₁₁

Acest fagure este unul dintre cele cinci faguri uniformi distincti construiți de grupul Coxeter . Simetria poate fi multiplicată cu simetria inelelor din diagramele Coxeter – Dynkin : ${\ displaystyle {\ tilde {A}} _ {3}}$

Faguri A3
Grup spațial	Fibrifold	Simetrie pătrată	Simetrie extinsă	Diagrama extinsă	Grup extins	Diagramele fagure de miere
F 4 3m (216)	1 ^o : 2	a1	[3 ^[4] ]		${\ displaystyle {\ tilde {A}} _ {3}}$	(Nici unul)
Fm 3 m (225)	2 ^- : 2	d2	<[3 ^[4] ]> ↔ [4,3 ^1,1 ]	↔	${\ displaystyle {\ tilde {A}} _ {3}}$ × 2 ₁ ↔ ${\ displaystyle {\ tilde {B}} _ {3}}$	₁ , ₂
Fd 3 m (227)	2 ⁺ : 2	g2	[[3 ^[4] ]] sau [2 ⁺ [3 ^[4] ]]	↔	${\ displaystyle {\ tilde {A}} _ {3}}$ × 2 ₂	₃
Pm 3 m (221)	4 ^- : 2	d4	<2 [3 ^[4] ]> ↔ [4,3,4]	↔	${\ displaystyle {\ tilde {A}} _ {3}}$ × 4 ₁ ↔ ${\ displaystyle {\ tilde {C}} _ {3}}$	₄
I 3 (204)	8 ^−o	r8	[4 [3 ^[4] ]] ⁺ ↔ [[4,3 ⁺ , 4]]	↔	½ × 8 ↔ ½ × 2 ${\ displaystyle {\ tilde {A}} _ {3}}$ ${\ displaystyle {\ tilde {C}} _ {3}}$	_(*)
Im 3 m (229)	8 ^o : 2	r8	[4 [3 ^[4] ]] ↔ [[4,3,4]]	↔	${\ displaystyle {\ tilde {A}} _ {3}}$ × 8 ↔ × 2 ${\ displaystyle {\ tilde {C}} _ {3}}$	₅

Fagure cubice rectificate

Fagure cubice rectificate
Tip	Fagure uniform
Simbolul Schläfli	r {4,3,4} sau t ₁ {4,3,4} r {4,3 ^1,1 } 2r {4,3 ^1,1 } r {3 ^[4] }
Diagramele Coxeter	= = = = =
Celulele	r {4,3} {3,4}
Fețe	triunghi {3} pătrat {4}
Figura Vertex	prisma pătrată
Notare Fibrifold din grupul spațial	Pm 3 m (221) 4 ^- : 2
Grupul Coxeter	${\ displaystyle {\ tilde {C}} _ {3}}$ , [4,3,4]
Dual	Celula octaedrică oblată :
Proprietăți	Vertex-tranzitiv , margine-tranzitiv

Fagure cubic rectificat sau cellulation cubic rectificat este uniform umplere spațiu tessellation (sau fagure ) în Euclidian 3-space. Este compus din octaedre și cuboctaedre într-un raport de 1: 1, cu o figură de vârf de prismă pătrată .

John Horton Conway numește acest fagure un cuboctahedrille , iar dualul său este un octahedrille oblat .

Proiecții

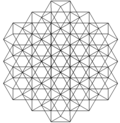
Fagurele cubi rectificat poate fi proiectat ortogonal în planul euclidiană cu diferite aranjamente de simetrie.

Proiecții ortogonale
Simetrie	p6m (* 632)	p4m (* 442)	pmm (* 2222)
Solid
Cadru

Simetrie

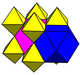
Există patru coloranți uniformi pentru celulele acestui fagure de miere cu simetrie reflectorizantă, enumerate după grupul lor Coxeter și numele construcției Wythoff și diagrama Coxeter de mai jos.

Simetrie	[4,3,4] ${\ displaystyle {\ tilde {C}} _ {3}}$	[1 ⁺ , 4,3,4] [4,3 ^1,1 ], ${\ displaystyle {\ tilde {B}} _ {3}}$	[4,3,4,1 ⁺ ] [4,3 ^1,1 ], ${\ displaystyle {\ tilde {B}} _ {3}}$	[1 ⁺ , 4,3,4,1 ⁺ ] [3 ^[4] ], ${\ displaystyle {\ tilde {A}} _ {3}}$
Grup spațial	Pm 3 m (221)	Fm 3 m (225)	Fm 3 m (225)	F 4 3m (216)
Colorare
Diagrama Coxeter
Diagrama Coxeter
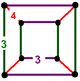
Figura Vertex
Vertex figura simetrie	D _4h [4,2] (* 224) ordinea 16	D _2h [2,2] (* 222) ordinea 8	C _4v [4] (* 44) ordinea 8	C _2v [2] (* 22) ordinea 4

Acest fagure poate fi împărțit pe planuri de plăci trihexagonale , folosind centrele hexagonale ale cuboctaedrelor, creând două cupole triunghiulare . Acest fagure scaliform este reprezentat de diagrama Coxeter, și simbolul s ₃ {2,6,3}, cu simetria notației coxeterului [2 ⁺ , 6,3].

.

Politopi înrudiți

O construcție de simetrie dublă poate fi realizată prin plasarea octaedrelor pe cuboctaedre, rezultând un fagure neuniform cu două tipuri de octaedre (octaedre regulate și antiprisme triunghiulare). Figura vertexului este un bifrust pătrat . Dualul este compus din bipiramide pătrate alungite .

Dual cell

Fagure cubic trunchiat

Fagure cubic trunchiat
Tip	Fagure uniform
Simbolul Schläfli	t {4,3,4} sau t _0,1 {4,3,4} t {4,3 ^1,1 }
Diagramele Coxeter	=
Tipul celulei	t {4,3} {3,4}
Tipul feței	triunghi {3} pătrat {4} octogon {8}
Figura Vertex	isoscel piramidă pătrată
Notare Fibrifold din grupul spațial	Pm 3 m (221) 4 ^- : 2
Grupul Coxeter	${\ displaystyle {\ tilde {C}} _ {3}}$ , [4,3,4]
Dual	Celula Pyramidille :
Proprietăți	Vertex-tranzitiv

Fagure cubic trunchiat sau cellulation cubic trunchiat este o uniformă de umplere spațiu tessellation (sau fagure ) în Euclidian 3-space. Este compus din cuburi trunchiate și octaedre într-un raport de 1: 1, cu o figură de vârf piramidă pătrată isoscelă .

John Horton Conway numește acest tip fagure o cubille trunchiată , și sa duală pyramidille .

Proiecții

Fagure cubic trunchiată poate fi proiectat ortogonal în planul euclidiană cu diferite aranjamente de simetrie.

Proiecții ortogonale
Simetrie	p6m (* 632)	p4m (* 442)	pmm (* 2222)
Solid
Cadru

Simetrie

Există o a doua colorare uniformă prin simetrie reflexivă a grupurilor Coxeter , a doua văzută cu celule cubice trunchiate alternativ colorate.

Constructie	Cubic alternativ bicantelat	Fagure cubic trunchiat
Grupul Coxeter	[4,3 ^1,1 ], ${\ displaystyle {\ tilde {B}} _ {3}}$	[4,3,4], = <[4,3 ^1,1 ]> ${\ displaystyle {\ tilde {C}} _ {3}}$
Grup spațial	Fm 3 m	Pm 3 m
Colorare
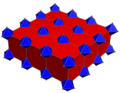
Diagrama Coxeter	=
Figura Vertex

Politopi înrudiți

O construcție de simetrie dublă poate fi realizată prin plasarea octaedrelor pe cuburile trunchiate, rezultând un fagure neuniform cu două tipuri de octaedre (octaedre regulate și antiprisme triunghiulare) și două tipuri de tetraedre (disfenoide tetragonale și disfenoide digonale). Figura vertexului este o cupolă pătrată octakis.

Figura Vertex

Dual cell

Fagure cubic bitruncat

Fagure cubic bitruncat

Tip	Fagure uniform
Simbolul Schläfli	2t {4,3,4} t _1,2 {4,3,4}
Diagrama Coxeter-Dynkin
Celulele	t {3,4}
Fețe	pătrat {4} hexagon {6}
Figura de margine	triunghi isoscel {3}
Figura Vertex	disfenoid tetragonal
Grupul de simetrie Notarea cu fibre multiple Notarea cu Coxeter	Im 3 m (229) 8 ^o : 2 [[4,3,4]]
Grupul Coxeter	${\ displaystyle {\ tilde {C}} _ {3}}$ , [4,3,4]
Dual	Tetraedrilă oblată Celulă fagure tetraedrică disfenoidă :
Proprietăți	Vertex-tranzitiv , margine-tranzitiv , celular-tranzitiv

Fagurele cubic bitruncat prezentat aici în raport cu un fagure cubic

Fagure cubic bitronconică este un spațiu de umplere tessellation (sau fagure ) în Euclidian 3-spațiu alcătuit din octoedre trunchiată (sau, echivalent, bitronconică cuburi). Are patru octaedre trunchiate în jurul fiecărui vârf, într-o figură de vârf disfenoid tetragonal . Fiind compus în întregime din octaedre trunchiate , este tranzitiv celular . De asemenea, este tranzitiv la margini , cu 2 hexagone și câte un pătrat pe fiecare margine și tranzitiv la vârf . Este unul dintre cei 28 de faguri uniformi .

John Horton Conway numește acest fagure de miere octaedrilă trunchiată în lista sa de teselare arhitectonică și catoptrică , cu dublul său numit tetraedrilă oblată , numită și fagure tetraedric disfenoid . Deși un tetraedru regulat nu poate țesui singur spațiul, acest dual are celule identice de tetraedru disfenoid cu fețe triunghiulare isoscel .

Proiecții

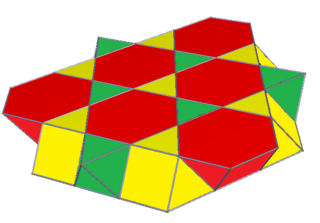
Fagure cubic bitronconică poate fi proiectat ortogonal în planul euclidiană cu diferite aranjamente de simetrie. Cea mai înaltă (hexagonală) formă de simetrie se proiectează într-o placă rombitrihexagonală neuniformă . O proiecție de simetrie pătrată formează două plăci pătrate trunchiate suprapuse , care se combină împreună ca plăci pătrate teșite .

Proiecții ortogonale
Simetrie	p6m (* 632)	p4m (* 442)	pmm (* 2222)
Solid
Cadru

Simetrie

Figura de vârf pentru acest fagure de miere este un tetraedru disfenoid și este, de asemenea, tetraedrul Goursat ( domeniul fundamental ) pentru grupul Coxeter . Acest fagure are patru construcții uniforme, celulele octaedrale trunchiate având diferite grupuri Coxeter și construcții Wythoff . Aceste simetrii uniforme pot fi reprezentate prin colorarea diferită a celulelor din fiecare construcție. ${\ displaystyle {\ tilde {A}} _ {3}}$

Cinci colorări uniforme pe celule
Grup spațial	Im 3 m (229)	Pm 3 m (221)	Fm 3 m (225)	F 4 3m (216)	Fd 3 m (227)
Fibrifold	8 ^o : 2	4 ^- : 2	2 ^- : 2	1 ^o : 2	2 ⁺ : 2
Grupul Coxeter	${\ displaystyle {\ tilde {C}} _ {3}}$ × 2 [[4,3,4]] = [4 [3 ^[4] ]] =	${\ displaystyle {\ tilde {C}} _ {3}}$ [4,3,4] = [2 [3 ^[4] ]] =	${\ displaystyle {\ tilde {B}} _ {3}}$ [4,3 ^1,1 ] = <[3 ^[4] ]> =	${\ displaystyle {\ tilde {A}} _ {3}}$ [3 ^[4] ]	${\ displaystyle {\ tilde {A}} _ {3}}$ × 2 [[3 ^[4] ]] = [[3 ^[4] ]]
Diagrama Coxeter
octaedre trunchiate	1	1: 1 :	2: 1: 1 : :	1: 1: 1: 1 : : :	1: 1 :
Figura Vertex
Vertex figura simetrie	[2 ⁺ , 4] (ordinul 8)	[2] (comanda 4)	[] (comanda 2)	[] ⁺ (comanda 1)	[2] ⁺ (ordinul 2)
Imagine colorată de celulă

Politopi înrudiți

Variantele neuniforme cu simetrie [4,3,4] și două tipuri de octaedre trunchiate pot fi dublate prin plasarea celor două tipuri de octaedre trunchiate pentru a produce un fagure neuniform cu octaedre trunchiate și prisme hexagonale (ca trapezoprisme ditrigonale). Figura sa de vârf este o bipiramidă triunghiulară asimetrică C _2v .

Acest fagure poate fi apoi alternat pentru a produce un alt fagure neuniform cu icosaedre piritoedrice , octaedre (ca antiprisme triunghiulare) și tetraedre (ca sfenoide). Figura sa de vârf are simetrie C _2v și este formată din 2 pentagone , 4 dreptunghiuri , 4 triunghiuri isoscele (împărțite în două seturi de 2) și 4 triunghiuri scalene .

Fagure cubic bitruncat alternativ

Fagure cubic bitruncat alternativ
Tip	Fagure convex
Simbolul Schläfli	2s {4,3,4} 2s {4,3 ^1,1 } sr {3 ^[4] }
Diagramele Coxeter	= = =
Celulele	{3,3} s {3,3}
Fețe	triunghi {3}
Figura Vertex
Grupul Coxeter	[[4,3 ⁺ , 4]], ${\ displaystyle {\ tilde {C}} _ {3}}$
Dual	Celulă cu fagure de zece diamante :
Proprietăți	Vertex-tranzitiv , neuniform

Alternat fagure cubic bitronconic sau fagure cubic bisnub este neuniformă, cu cea mai mare construcție de simetrie reflectând o alternanta de uniforma bitronconică fagure cubi. O construcție cu simetrie inferioară implică icosahedra regulată asociată cu icosahedra aurie (cu 8 triunghiuri echilaterale împerecheate cu 12 triunghiuri aurii). Există trei construcții din trei diagrame Coxeter legate :, , și . Acestea au simetrie [4,3 ⁺ , 4], [4, (3 ^1,1 ) ⁺ ] și respectiv [3 ^[4] ] ⁺ . Prima și ultima simetrie pot fi dublate ca [[4,3 ⁺ , 4]] și [[3 ^[4] ]] ⁺ .

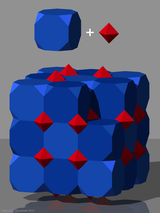
Acest fagure este reprezentat în atomii de bor ai cristalului α-rombihedric . Centrele icosahedra sunt situate la pozițiile fcc ale zăbrelei.

Cinci coloranți uniformi
Grup spațial	I 3 (204)	Pm 3 (200)	Fm 3 (202)	Fd 3 (203)	F23 (196)
Fibrifold	8 ^−o	4 ^-	2 ^-	2 ^{o +}	1 ^o
Grupul Coxeter	[[4,3 ⁺ , 4]]	[4,3 ⁺ , 4]	[4, (3 ^1,1 ) ⁺ ]	[[3 ^[4] ]] ⁺	[3 ^[4] ] ⁺
Diagrama Coxeter
Ordin	dubla	deplin	jumătate	sfert dublu	sfert

Fagure cubice cantelate

Fagure cubice cantelate
Tip	Fagure uniform
Simbolul Schläfli	rr {4,3,4} sau t _0,2 {4,3,4} rr {4,3 ^1,1 }
Diagrama Coxeter	=
Celulele	rr {4,3} r {4,3} {} x {4}
Figura Vertex	pană
Notare Fibrifold din grupul spațial	Pm 3 m (221) 4 ^- : 2
Grupul Coxeter	[4,3,4], ${\ displaystyle {\ tilde {C}} _ {3}}$
Dual	Celulă octaedrică oblată sfert :
Proprietăți	Vertex-tranzitiv

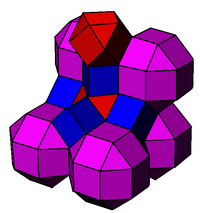
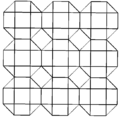
Fagure cubic cantellated sau cellulation cubic cantellated este o uniformă de umplere spațiu tessellation (sau fagure ) în Euclidian 3-space. Este compus din rombicuboctaedre , cuboctaedre și cuburi într-un raport de 1: 1: 3, cu o figură de vârf de pană .

John Horton Conway numește acest fagure de miere 2-RCO-trille și octaedrila sa oblală duală .

Imagini

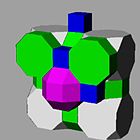
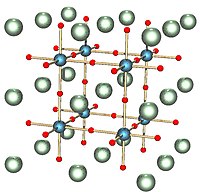	Este strâns legat de structura perovskitei , prezentată aici cu simetrie cubică, cu atomi așezați în centrul celulelor acestui fagure de miere.

Proiecții

Fagure cubic cantellated poate fi proiectat ortogonal în planul euclidiană cu diferite aranjamente de simetrie.

Proiecții ortogonale
Simetrie	p6m (* 632)	p4m (* 442)	pmm (* 2222)
Solid
Cadru

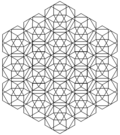
Simetrie

Există o a doua colorare uniformă prin simetrie reflecțională a grupurilor Coxeter , a doua văzută cu celule rombicuboctaedrice colorate alternativ.

Culori uniforme de vertex după celulă
Constructie	Fagure cubic trunchiat	Cubic alternativ bicantelat
Grupul Coxeter	[4,3,4], = <[4,3 ^1,1 ]> ${\ displaystyle {\ tilde {C}} _ {3}}$	[4,3 ^1,1 ], ${\ displaystyle {\ tilde {B}} _ {3}}$
Grup spațial	Pm 3 m	Fm 3 m
Diagrama Coxeter
Colorare
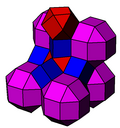
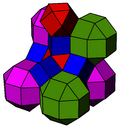
Figura Vertex
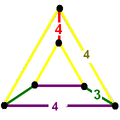
Vertex figura simetrie	[] ordinea 2	[] ⁺ comanda 1

Politopi înrudiți

O construcție dublă simetrie poate fi realizată prin plasarea cuboctaedrelor pe rombicuboctahedra, ceea ce are ca rezultat fagurele cubic rectificat , luând golurile antiprismului triunghiular ca octaedre regulate , perechi antiprism pătrate și disfenoide tetragonale cu înălțime zero ca componente ale cuboctaedrului . Alte variante au ca rezultat cuboctaedre , antiprisme pătrate , octaedre (ca antipodii triunghiulare) și tetraedre (ca defenoide tetragonale), cu o figură de vârf echivalentă topologic cu un cub cu o prismă triunghiulară atașată la una dintre fețele sale pătrate.

Sfert de octaedru oblat

Dualul fagurelui cubic cantelat se numește un sfert de octaedră oblată , o teselare catoptrică cu diagramă Coxeter , conținând fețe din două din cele patru hiperplanuri ale domeniului fundamental cubic [4,3,4].

Are celule bipiramidice triunghiulare neregulate care pot fi văzute ca 1/12 dintr-un cub, realizat din centrul cubului, 2 centre de față și 2 vârfuri.

Fagure cubice cantitruncate

Fagure cubice cantitruncate
Tip	Fagure uniform
Simbolul Schläfli	tr {4,3,4} sau t _0,1,2 {4,3,4} tr {4,3 ^1,1 }
Diagrama Coxeter	=
Celulele	tr {4,3} t {3,4} {} x {4}
Fețe	pătrat {4} hexagon {6} octogon {8}
Figura Vertex	sfenoid oglindit
Grupul Coxeter	[4,3,4], ${\ displaystyle {\ tilde {C}} _ {3}}$
Grupul de simetrie Notarea cu fibră pliabilă	Pm 3 m (221) 4 ^- : 2
Dual	celule piramidil triunghiulare :
Proprietăți	Vertex-tranzitiv

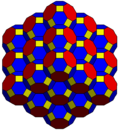
Fagure cubic cantitruncated sau cellulation cubic cantitruncated este o uniformă de umplere spațiu tessellation (sau fagure ) în Euclidian 3-space, format din cuboctahedra trunchiată , octoedre trunchiat și cuburi într - un raport de 1: 1: 3, cu un sfenoid oglindit figura vârfului .

John Horton Conway numește acest fagure un n-tCO-trille și piramidilul său triunghiular dublu .

Imagini

Există patru celule în jurul fiecărui vârf:

Proiecții

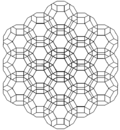
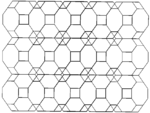
Fagure cubic cantitruncated poate fi proiectat ortogonal în planul euclidiană cu diferite aranjamente de simetrie.

Proiecții ortogonale
Simetrie	p6m (* 632)	p4m (* 442)	pmm (* 2222)
Solid
Cadru

Simetrie

Celulele pot fi prezentate în două simetrii diferite. Formularul liniar al diagramei Coxeter poate fi desenat cu o culoare pentru fiecare tip de celulă. Forma de diagramă bifurcantă poate fi desenată cu două tipuri (culori) de celule de cuboctaedru trunchiate alternând.

Constructie	Cubic cantitruncat	Cub alternativ omnitruncat
Grupul Coxeter	[4,3,4], = <[4,3 ^1,1 ]> ${\ displaystyle {\ tilde {C}} _ {3}}$	[4,3 ^1,1 ], ${\ displaystyle {\ tilde {B}} _ {3}}$
Grup spațial	Pm 3 m (221)	Fm 3 m (225)
Fibrifold	4 ^- : 2	2 ^- : 2
Colorare
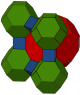
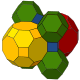
Diagrama Coxeter
Figura Vertex
Vertex figura simetrie	[] ordinea 2	[] ⁺ comanda 1

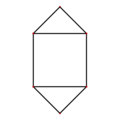
Piramidilă triunghiulară

Dualul fagurelui cubic cantitruncat se numește piramidilă triunghiulară , cu diagrama Coxeter ,. Aceste celule fagure de miere reprezintă domeniile fundamentale ale simetriei. ${\ displaystyle {\ tilde {B}} _ {3}}$

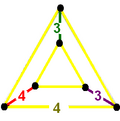
O celulă poate fi la fel de 1/24 dintr-un cub de translație cu vârfurile poziționate: luând două colț, centrul feței ne și centrul cubului. Culorile și etichetele marginii specifică câte celule există în jurul marginii.

Poliedre și faguri înrudiți

Este legat de un apeiroedru înclinat cu configurația vârfului 4.4.6.6, cu octogonele și unele dintre pătrate îndepărtate. Poate fi văzut ca fiind construit prin mărirea celulelor cuboctaedrice trunchiate sau prin mărirea octaedrelor și cuburilor trunchiate alternate.

Două vederi

Politopi înrudiți

O construcție de simetrie dublă poate fi realizată prin plasarea octaedrelor trunchiate pe cuboctaedrele trunchiate, rezultând un fagure neuniform cu octaedre trunchiate , prisme hexagonale (ca trapezoprisme ditrigonale), cuburi (ca prisme pătrate), prisme triunghiulare (ca pene simetrice C _2v ) , și tetraedre (ca defenoide tetragonale). Figura sa de vârf este echivalentă topologic cu octaedrul .

Figura Vertex

Dual cell

Fagure cubic alternativ cantitruncat

Fagure cubic alternativ cantitruncat
Tip	Fagure convex
Simbolul Schläfli	sr {4,3,4} sr {4,3 ^1,1 }
Diagramele Coxeter	=
Celulele	s {4,3} s {3,3} {3,3}
Fețe	triunghi {3} pătrat {4}
Figura Vertex
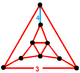
Grupul Coxeter	[(4,3) ⁺ , 4]
Dual	Celula:
Proprietăți	Vertex-tranzitiv , neuniform

Alternat fagure cubic cantitruncated sau cârn rectificat fagure cubic conține trei tipuri de celule: cuburi cârn , icosahedra (cu T _h simetrie), tetraedre (ca disphenoids tetragonale) și noi celule tetraedrice create la golurile.
Deși nu este uniformă, în mod constructiv poate fi dată ca diagrame Coxeter sau .

Deși este neuniformă, există o versiune near-miss cu două lungimi de margine prezentate mai jos, dintre care una este cu aproximativ 4,3% mai mare decât cealaltă. Cuburile de snub în acest caz sunt uniforme, dar restul celulelor nu.

Fagure cubic cubic

Fagure cubic ortosnub
Tip	Fagure convex
Simbolul Schläfli	2s ₀ {4,3,4}
Diagramele Coxeter
Celulele	s ₂ {3,4} s {3,3} {} x {3}
Fețe	triunghi {3} pătrat {4}
Figura Vertex
Grupul Coxeter	[4 ⁺ , 3,4]
Dual	Celula:
Proprietăți	Vertex-tranzitiv , neuniform

Fagure cubic carn cantic este construit prin snubbing octoedrele trunchiate într - un mod care frunzele doar dreptunghiuri de cuburi (prisme pătrate). Nu este uniformă, dar poate fi reprezentată ca diagramă Coxeter . Are rombicuboctaedre (cu simetrie T _h ), icosaedre (cu simetrie T _h ) și prisme triunghiulare (ca pene de simetrie C _2v ) care umple golurile.

Politopi înrudiți

O construcție de simetrie dublă poate fi realizată prin plasarea icosahedrelor pe rombicuboctahedra, rezultând un fagure neuniform cu icosahedra , octaedre (ca antiprisme triunghiulare), prisme triunghiulare (ca pene asimetrice C _2v ) și piramide pătrate .

Figura Vertex

Dual cell

Fagure cubic runcitruncat

Fagure cubic runcitruncat
Tip	Fagure uniform
Simbolul Schläfli	t _0,1,3 {4,3,4}
Diagramele Coxeter
Celulele	rr {4,3} t {4,3} {} x {8} {} x {4}
Fețe	triunghi {3} pătrat {4} octogon {8}
Figura Vertex	piramida izoscel-trapezoidală
Grupul Coxeter	[4,3,4], ${\ displaystyle {\ tilde {C}} _ {3}}$
Notare Fibrifold din grupul spațial	Pm 3 m (221) 4 ^- : 2
Dual	celulă piramidilă sfert pătrat
Proprietăți	Vertex-tranzitiv

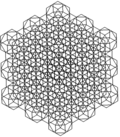
Fagure cubic runcitruncated sau cellulation cubic runcitruncated este uniform tessellation-umplere spațiu (sau fagure ) în Euclidian 3-space. Este compus din rombicuboctaedre , cuburi trunchiate , prisme octogonale și cuburi într-un raport de 1: 1: 3: 3, cu o figură de vârf de piramidă isoscel-trapezoidală .

Numele său este derivat din diagrama Coxeter ,cu trei noduri inelate reprezentând 3 oglinzi active în construcția Wythoff din relația sa cu fagurele cubic obișnuit .

John Horton Conway numește acest fagure de miere 1-RCO-trille , și dublu pătrat pătrat piramidilă .

Proiecții

Fagure cubic runcitruncated poate fi proiectat ortogonal în planul euclidiană cu diferite aranjamente de simetrie.

Proiecții ortogonale
Simetrie	p6m (* 632)	p4m (* 442)	pmm (* 2222)
Solid
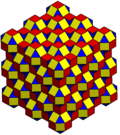
Cadru

Apeiroedru asimetric asociat

Există doi apeiroedri uniformi asemănători , cu același aranjament de vârf , văzut ca celule limită dintr-un subset de celule. Unul are triunghiuri și pătrate, iar celălalt triunghiuri, pătrate și octogonuri.

Piramidilă pătrată pătrată

Dualul către fagurele cubic runcitruncat se numește un sfert pătrat piramidil , cu diagrama Coxeter . Fețele există în 3 din 4 hiperplanuri din grupul [4,3,4], Coxeter. ${\ displaystyle {\ tilde {C}} _ {3}}$

Celulele sunt piramide neregulate și pot fi văzute ca 1/24 dintr-un cub, folosind un colț, un punct de margine mijlocie, două centre de față și centrul cubului.

Politopi înrudiți

O construcție de simetrie dublă poate fi realizată prin plasarea rombicuboctaedrelor pe cuburile trunchiate, rezultând un fagure neuniform cu rombicuboctaedre , octaedre (ca antiprisme triunghiulare), cuburi (ca prisme pătrate), două tipuri de prisme triunghiulare (ambele pene simetrice C _2v ) , și tetraedre (ca defenoide digonale). Figura sa de vârf este echivalentă topologic cu prisma triunghiulară mărită .

Figura Vertex

Dual cell

Fagure cubic omnitruncat

Fagure cubic omnitruncat
Tip	Fagure uniform
Simbolul Schläfli	t _0,1,2,3 {4,3,4}
Diagrama Coxeter
Celulele	tr {4,3} {} x {8}
Fețe	pătrat {4} hexagon {6} octogon {8}
Figura Vertex	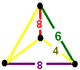disfenoid filic
Grupul de simetrie Notarea cu fibre multiple Notarea cu Coxeter	Im 3 m (229) 8 ^o : 2 [[4,3,4]]
Grupul Coxeter	[4,3,4], ${\ displaystyle {\ tilde {C}} _ {3}}$
Dual	a opta celulă piramidilă
Proprietăți	Vertex-tranzitiv

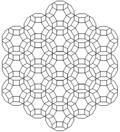
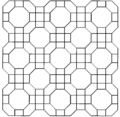
Fagure cubic omnitruncated sau cellulation cubic omnitruncated este o uniformă de umplere spațiu tessellation (sau fagure ) în Euclidian 3-space. Este compus din cuboctaedre trunchiate și prisme octogonale într-un raport de 1: 3, cu o figură de vârf disphenoid filic .

John Horton Conway numește acest fagure de miere b-tCO-trille și cel de -al doilea al optulea piramidil .

Proiecții

Fagure cubic omnitruncated poate fi proiectat ortogonal în planul euclidiană cu diferite aranjamente de simetrie.

Proiecții ortogonale
Simetrie	p6m (* 632)	p4m (* 442)	pmm (* 2222)
Solid
Cadru

Simetrie

Celulele pot fi prezentate în două simetrii diferite. Forma diagramei Coxeter are două culori de cuboctaedre trunchiate și prisme octogonale . Simetria poate fi dublată prin raportarea primei și ultimei ramuri ale diagramei Coxeter, care poate fi afișată cu o singură culoare pentru toate celulele de prismă cuboctaedrică și octogonală trunchiate.

Două colorări uniforme
Simetrie	${\ displaystyle {\ tilde {C}} _ {3}}$ , [4,3,4]	${\ displaystyle {\ tilde {C}} _ {3}}$ × 2, [[4,3,4]]
Grup spațial	Pm 3 m (221)	Im 3 m (229)
Fibrifold	4 ^- : 2	8 ^o : 2
Colorare
Diagrama Coxeter
Figura Vertex

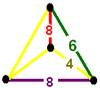
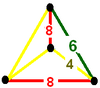
Poliedre înrudite

Există două apeiroedre uniforme asemănătoare , cu același aranjament de vârf . Primul are octogonuri eliminate și configurația vârfului 4.4.4.6. Poate fi văzut ca cuboctaedre trunchiate și prisme octogonale mărite împreună. Al doilea poate fi văzut ca prisme octogonale mărite, configurația vârfului 4.8.4.8.

4.4.4.6	4.8.4.8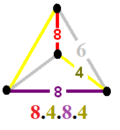

Politopi înrudiți

Variantele neuniforme cu [4,3,4] simetrie și două tipuri de cuboctaedre trunchiate pot fi dublate prin plasarea celor două tipuri de cuboctahedra trunchiate unul pe altul pentru a produce un fagure neuniform cu cuboctahedra trunchiat , prisme octogonale , prisme hexagonale (sub formă de trapezoprisme ditrigonale) și două tipuri de cuburi (ca trapezoprisme dreptunghiulare și variantele lor simetrice C _2v ). Figura sa de vârf este o bipiramidă triunghiulară neregulată .

Figura Vertex

Dual cell

Acest fagure poate fi apoi alternat pentru a produce un alt fagure neuniform cu cuburi de snub , antiprisme pătrate , octaedre (ca antiprisme triunghiulare) și trei tipuri de tetraedre (ca defenoide tetragonale, defenoide filice și tetraedre neregulate).

Figura Vertex

Fagure cubic omnitruncat cubic

Fagure cubic omnitruncat cubic
Tip	Fagure convex
Simbolul Schläfli	ht _0,1,2,3 {4,3,4}
Diagrama Coxeter
Celulele	s {4,3} s {2,4} {3,3}
Fețe	triunghi {3} pătrat {4}
Figura Vertex
Simetrie	[[4,3,4]] ⁺
Dual	Fagure cubic alternativ omnitruncat dual
Proprietăți	Vertex-tranzitiv , neuniform

Un fagure cub alternativ omnitruncat sau un fagure cub omnisnub poate fi construit prin alternarea fagurelui cub omnitruncat, deși nu poate fi uniformizat, dar i se poate da diagrama Coxeter :și are simetrie [[4,3,4]] ⁺ . Face cuburi din cuboctaedrele trunchiate , antiprisme pătrate din prismele octogonale și creează noi celule tetraedrice din goluri.

Fagure cubic alternativ omnitruncat dual

Fagure cubic alternativ omnitruncat dual
Tip	Fagure uniforme alternate duale
Simbolul Schläfli	DHT _0,1,2,3 {4,3,4}
Diagrama Coxeter
Celula
Cifre de vârf	pentagonal icositetraedru tetragonal trapezohedron tetrahedron
Simetrie	[[4,3,4]] ⁺
Dual	Fagure cubic omnitruncat cubic
Proprietăți	Celulă tranzitivă

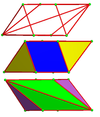
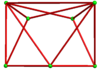
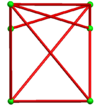
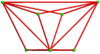
Un fagure cubic alternativ omnitruncat alternativ este un fagure cu umplere de spațiu construit ca dual al fagurelui cubic omnitruncat alternativ .

24 de celule se potrivesc în jurul unui vârf, făcând o simetrie chirală octaedrică care poate fi stivuită în toate cele 3 dimensiuni:

Celulele individuale au simetrie de rotație de două ori. În proiecția ortogonală 2D, aceasta arată ca o simetrie oglindă.

Vizualizări celulare
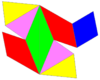Net

Fagure cubic cantitruncat cubic

Fagure cubic cantitruncat cubic
Tip	Fagure convex
Simbolul Schläfli	sr ₃ {4,3,4}
Diagramele Coxeter
Celulele	s ₂ {3,4} s {4,3} {} x {4} {} x {3}
Fețe	triunghi {3} pătrat {4}
Figura Vertex
Grupul Coxeter	[4,3 ⁺ , 4]
Dual	Celula: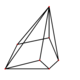
Proprietăți	Vertex-tranzitiv , neuniform

Runcic cantitruncated fagure cubic sau runcic cellulation cubic cantitruncated este construită prin îndepărtarea alternarea dreptunghiuri lungi din octogoane și nu este uniformă, dar poate fi reprezentat ca diagrama Coxeter . Are rombicuboctaedre (cu simetrie T _h ), cuburi snub , două tipuri de cuburi : prisme pătrate și trapezoprisme dreptunghiulare (echivalente topologic cu un cub, dar cu simetrie D _2d ) și prisme triunghiulare (ca pene de simetrie C _2v ) care umple golurile .

Fagure cubice Biorthosnub

Fagure cubic Biorthosnub
Tip	Fagure convex
Simbolul Schläfli	2s _0,3 {4,3,4}
Diagramele Coxeter
Celulele	s ₂ {3,4} {} x {4}
Fețe	triunghi {3} pătrat {4}
Figura Vertex	( Anti-pană tetragonală )
Grupul Coxeter	[[4,3 ⁺ , 4]]
Dual	Celula:
Proprietăți	Vertex-tranzitiv , neuniform

Fagure cubic biorthosnub este construită prin îndepărtarea alternarea dreptunghiuri lungi din octogoane ortogonală și nu este uniformă, dar poate fi reprezentat ca diagrama Coxeter . Are rombicuboctaedre (cu simetrie T _h ) și două feluri de cuburi : prisme pătrate și trapezoprisme dreptunghiulare (echivalente topologic cu un cub, dar cu simetrie D _2d ).

Fagure prismatic pătrat trunchiat

Fagure prismatic pătrat trunchiat
Tip	Fagure uniform
Simbolul Schläfli	t {4,4} × {∞} sau t _0,1,3 {4,4,2, ∞} tr {4,4} × {∞} sau t _0,1,2,3 {4,4, ∞}
Diagrama Coxeter-Dynkin
Celulele	{} x {8} {} x {4}
Fețe	pătrat {4} octogon {8}
Grupul Coxeter	[4,4,2, ∞]
Dual	Celula de placare prismatică pătrată Tetrakis :
Proprietăți	Vertex-tranzitiv

Trunchiate fagure prismatică pătrat sau -tomo pătrat cellulation prismatic este un spațiu de umplere tessellation (sau fagure ) în Euclidian 3-space . Este compus din prisme octogonale și cuburi într-un raport de 1: 1.

Este construit dintr-o placă pătrată trunchiată extrudată în prisme.

Este unul dintre cei 28 de faguri uniformi conveși .

Snub fagure prismatic pătrat

Snub fagure prismatic pătrat
Tip	Fagure uniform
Simbolul Schläfli	s {4,4} × {∞} sr {4,4} × {∞}
Diagrama Coxeter-Dynkin
Celulele	{} x {4} {} x {3}
Fețe	triunghi {3} pătrat {4}
Grupul Coxeter	[4 ⁺ , 4,2, ∞] [(4,4) ⁺ , 2, ∞]
Dual	Celulă fagure prismatice pentagonale din Cairo :
Proprietăți	Vertex-tranzitiv

Cârn pătrat fagure prismatică sau cellulation prismatic simo-pătrat este un spațiu de umplere tessellation (sau fagure ) în Euclidian 3-space . Este compus din cuburi și prisme triunghiulare într-un raport de 1: 2.

Este construit dintr-o plăcuță pătrată, extrudată în prisme.

Este unul dintre cei 28 de faguri uniformi conveși .

Fagure antiprismatic pătrat

Fagure antiprismatic pătrat
Tip	Fagure convex
Simbolul Schläfli	ht _1,2,3 {4,4,2, ∞} ht _0,1,2,3 {4,4, ∞}
Diagrama Coxeter-Dynkin
Celulele	s {2,4} {3,3}
Fețe	triunghi {3} pătrat {4}
Figura Vertex
Simetrie	[4,4,2, ∞] ⁺
Proprietăți	Vertex-tranzitiv , neuniform

Un fagure antiprismatic pătrat poate fi construit prin alternarea fagurelui prismatic pătrat trunchiat, deși nu poate fi uniformizat, dar i se poate da diagrama Coxeter :și are simetrie [4,4,2, ∞] ⁺ . Face antiprisme pătrate din prismele octogonale , tetraedre (ca defenoide tetragonale) din cuburi și două tetraedre din bipiramidele triunghiulare .

Vezi si

Teselare arhitectonică și catoptrică
Fagure cubic alternativ
Lista politopilor obișnuiți
Order-5 fagure cubice Un fagure cub hiperbolic cu 5 cuburi pe margine
voxel

Referințe

John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss , (2008) The Symmetries of Things , ISBN 978-1-56881-220-5 (Capitolul 21, Denumirea poliedrelor și a plăcilor arhimediene și catalane, teselări arhitectonice și catoptrice, p 292-298, include toate formele neprismatice)
Coxeter, HSM Regular Polytopes , (ediția a 3-a, 1973), ediția Dover, ISBN 0-486-61480-8 p. 296, Tabelul II: Faguri regulate
George Olshevsky, Uniform Panoploid Tetracombs , Manuscript (2006) (Lista completă a 11 plăci uniforme convexe, 28 faguri uniformi conveși și 143 tetracombe uniforme convexe)
Branko Grünbaum , Tiglă uniformă de 3 spații. Geombinatorics 4 (1994), 49 - 56.
Kaleidoscopes: Selected Writings of HSM Coxeter , editat de F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Lucrarea 22) HSM Coxeter, Politopi regulat și semi regulat I , [Mat. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Plombe uniforme)
A. Andreini , Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corespondative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
Klitzing, Richard. "Faguri 3D euclidieni x4o3o4o - chon - O1" .
Faguri uniformi în 3 spații: 01-Chon

v t e Faguri de bază, convexe, regulate și uniforme, în dimensiunile 2-9
Spaţiu	Familie	${\ displaystyle {\ tilde {A}} _ {n-1}}$	${\ displaystyle {\ tilde {C}} _ {n-1}}$	${\ displaystyle {\ tilde {B}} _ {n-1}}$	${\ displaystyle {\ tilde {D}} _ {n-1}}$	${\ displaystyle {\ tilde {G}} _ {2}}$ / / ${\ displaystyle {\ tilde {F}} _ {4}}$ ${\ displaystyle {\ tilde {E}} _ {n-1}}$
E ²	Placi uniforme	{3 ^[3] }	δ ₃	hδ ₃	qδ ₃	Hexagonal
E ³	Fagure convex uniform	{3 ^[4] }	δ ₄	hδ ₄	qδ ₄
E ⁴	Uniform cu 4 faguri de miere	{3 ^[5] }	δ ₅	hδ ₅	qδ ₅	Fagure cu 24 de celule
E ⁵	Uniform cu 5 faguri de miere	{3 ^[6] }	δ ₆	hδ ₆	qδ ₆
E ⁶	Uniform cu 6 faguri de miere	{3 ^[7] }	δ ₇	hδ ₇	qδ ₇	2 ₂₂
E ⁷	Uniform cu 7 faguri de miere	{3 ^[8] }	δ ₈	hδ ₈	qδ ₈	1 ₃₃ • 3 ₃₁
E ⁸	Uniform 8 faguri	{3 ^[9] }	δ ₉	hδ ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
E ⁹	Uniform cu 9 faguri de miere	{3 ^[10] }	δ ₁₀	hδ ₁₀	qδ ₁₀
E ¹⁰	Uniform cu 10 faguri de miere	{3 ^[11] }	δ ₁₁	hδ ₁₁	qδ ₁₁
E ^{n -1}	Uniform ( n -1) - fagure de miere	{3 ^[n] }	δ _n	hδ _n	qδ _n	1 _k2 • 2 _k1 • k ₂₁

Languages

In other projects

Fagure cubice - Cubic honeycomb

Faguri înrudiți

Izometriile rețelelor cubice simple

Coloranți uniformi

Proiecții

Politopi și faguri asociați

Politopi înrudiți

Teselări euclidiene înrudite

Fagure cubice rectificate

Proiecții

Simetrie

Politopi înrudiți

Fagure cubic trunchiat

Proiecții

Simetrie

Politopi înrudiți

Fagure cubic bitruncat

Proiecții

Simetrie

Politopi înrudiți

Fagure cubic bitruncat alternativ

Fagure cubice cantelate

Imagini

Proiecții

Simetrie

Politopi înrudiți

Sfert de octaedru oblat

Fagure cubice cantitruncate

Imagini

Proiecții

Simetrie

Piramidilă triunghiulară

Poliedre și faguri înrudiți

Politopi înrudiți

Fagure cubic alternativ cantitruncat

Fagure cubic cubic

Politopi înrudiți

Fagure cubic runcitruncat

Proiecții

Apeiroedru asimetric asociat

Piramidilă pătrată pătrată

Politopi înrudiți

Fagure cubic omnitruncat

Proiecții

Simetrie

Poliedre înrudite

Politopi înrudiți

Fagure cubic omnitruncat cubic

Fagure cubic alternativ omnitruncat dual

Fagure cubic cantitruncat cubic

Fagure cubice Biorthosnub

Fagure prismatic pătrat trunchiat

Snub fagure prismatic pătrat

Fagure antiprismatic pătrat

Vezi si

Referințe